题目内容
数列1，1+2，1+2+22，…，1+2+22+…+2n－1，…的前n项和为（ ）
A.2n－n－1 B.2n+1－n－2
C.2n D.2n+1－n
【答案】
B
【解析】因为根据题意可知，1+2+22+…+2n－1=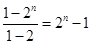
，因此通项公式是由等差数列和等比数列的和，利用等比数列和等差数列的前n项和得到和式为2n+1－n－2，选B.
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
数列1、1+2、1+2+22、…、1+2+22+…+2n-1…的前n项和为 （ ）
| A．2n—n—1 | B．2n+1—n—2 | C．2n | D．2n+1—n |