题目内容
1．若复数$z=\frac{1+i}{1-i}，则{z^{2010}}$=-1．分析 根据复数的基本运算法则进行求解即可．
解答 解：z=$\frac{1+i}{1-i}$，则z2=（$\frac{1+i}{1-i}$）2=$\frac{（1+i）^{2}}{（1-i）^{2}}=\frac{2i}{-2i}=-1$，
则z2010=（z2）1005=（-1）1005=-1，
故答案为：-1．
点评 本题主要考查复数的基本运算，先计算z2=-1是解决本题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
16．
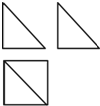利用一球体毛坯切削后得到一个几何体，该几何体的三视图如图所示，若主视图和左视图都是直角边长为1的等腰直角三角形，则毛坯球体的体积最小应为（ ）
利用一球体毛坯切削后得到一个几何体，该几何体的三视图如图所示，若主视图和左视图都是直角边长为1的等腰直角三角形，则毛坯球体的体积最小应为（ ）| A． | $\frac{{\sqrt{2}π}}{3}$ | B． | $\frac{4π}{3}$ | C． | $\frac{\sqrt{3}π}{2}$ | D． | $\frac{8\sqrt{2}π}{3}$ |
6．设f°（x）=cosx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn（x）=f′n-1（x）（n∈N*），则f2011（x）=（ ）
| A． | cosx | B． | -sinx | C． | -cosx | D． | sinx |
13．在△ABC中，A，B是三角形的内角，且A=90°，若$\overrightarrow{AB}$=（2，-1），$\overrightarrow{AC}$=（sinB，$\sqrt{3}$），则角B等于（ ）
| A． | 30° | B． | 60° | C． | 60°或120° | D． | 30°或150° |