题目内容
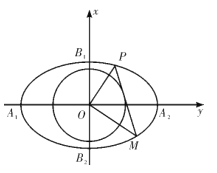
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.
【答案】(1)![]() ;(2)(i)详见解析;(ii)是定值
;(2)(i)详见解析;(ii)是定值![]() .
.
【解析】
(1)由已知可得:直线![]() 的方程为:
的方程为:![]() ,利用四边形
,利用四边形![]() 的内切圆为
的内切圆为![]() 可求得内切圆的半径
可求得内切圆的半径![]() ,问题得解。
,问题得解。
(2)(i)设切线![]() ,联立直线方程与椭圆方程可得:
,联立直线方程与椭圆方程可得: ,即可求得
,即可求得 ,所以
,所以![]() ,问题得证。
,问题得证。
(ii)①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,②当直线
,②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,联立直线方程与椭圆方程可得:
,联立直线方程与椭圆方程可得:![]() ,即可求得:
,即可求得: ,同理可得:
,同理可得: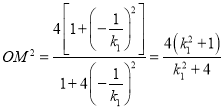 ,问题得解。
,问题得解。
(1)因为![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的右顶点和上顶点,则
的右顶点和上顶点,则![]() ,
,![]() 坐标分别为
坐标分别为![]() ,可得直线
,可得直线![]() 的方程为:
的方程为:![]()
则原点O到直线![]() 的距离为
的距离为![]() ,则圆
,则圆![]() 的半径
的半径![]() ,
,
故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)(i)可设切线![]() ,
,
将直线![]() 的方程代入椭圆
的方程代入椭圆![]() 可得
可得![]() ,由韦达定理得:
,由韦达定理得:
 则
则 ,
,
又![]() 与圆
与圆![]() 相切,可知原点O到
相切,可知原点O到![]() 的距离
的距离![]() ,整理得
,整理得![]() ,
,
则 ,所以
,所以![]() ,故
,故![]() .
.
(ii)由![]() 知
知![]() ,
,
①当直线![]() 的斜率不存在时,显然
的斜率不存在时,显然![]() ,此时
,此时![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]()
代入椭圆方程可得![]() ,则
,则![]() ,
,
故 ,
,
同理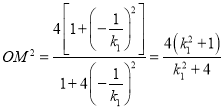 ,
,
则 .
.
综上可知:![]() 为定值.
为定值.

【题目】为了保障某种药品的主要药理成分在国家药品监督管理局规定的值范围内,某制药厂在该药品的生产过程中,检验员在一天中按照规定每间隔2小时对该药品进行检测,每天检测4次:每次检测由检验员从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的其主要药理成分含量服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示某次抽取的20件产品中其主要药理成分含量在
表示某次抽取的20件产品中其主要药理成分含量在![]() 之外的药品件数,求
之外的药品件数,求![]() (精确到0.001)及
(精确到0.001)及![]() 的数学期望;
的数学期望;
(2)在一天内四次检测中,如果有一次出现了主要药理成分含量在![]() 之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查;如果在一天中,有连续两次检测出现了主要药理成分含量在
之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查;如果在一天中,有连续两次检测出现了主要药理成分含量在![]() 之外的药品,则需停止生产并对原材料进行检测.
之外的药品,则需停止生产并对原材料进行检测.
①下面是检验员在某一次抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() ,
,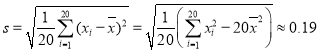 .其中
.其中![]() 为抽取的第
为抽取的第![]() 件药品的主要药理成分含量,
件药品的主要药理成分含量,![]() .用样本平均数
.用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
②试确定一天中需停止生产并对原材料进行检测的概率(精确到0.001).附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,
![]() .
.
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.