题目内容
【题目】如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,平面PAC垂直圆O所在平面,直线PC与圆O所在平面所成角为60°,PA⊥PC.
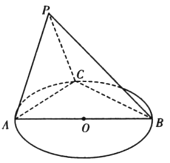
(1)证明:AP⊥平面PBC
(2)求二面角P—AB一C的余弦值
【答案】(1)见解析.(2) ![]() .
.
【解析】
(1)由已知条件得BC⊥平面PAC,可得![]() 又
又![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)法一:过![]() 作
作![]() 于
于![]() ,由平面
,由平面![]() 平面
平面![]() ,知∠HCP为直线
,知∠HCP为直线![]() 与圆
与圆![]() 所在平面所成角,可得
所在平面所成角,可得![]() ,由此能得到
,由此能得到![]() 为二面角
为二面角![]() 的平面角.利用平面几何知识求解即可.
的平面角.利用平面几何知识求解即可.
法二:利用空间向量法求解线面角.
(1)由已知可知![]() ,又平面
,又平面![]() 平面圆
平面圆![]() ,平面
,平面![]() 平面圆
平面圆![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)法一:过![]() 作
作![]() 于
于![]() ,由于平面
,由于平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,
则![]() 为直线
为直线![]() 与圆
与圆![]() 所在平面所成角,所以
所在平面所成角,所以![]() .
.
过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() ,
,
故![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由已知![]() ,
,![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
由![]() 得
得![]() ,在
,在![]() 中,
中,![]() ,
,
故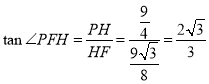 ,故
,故![]() ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.
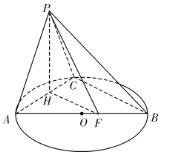
法二:过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
, ,
, ,
,![]() ,
,
从而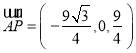 ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则 得
得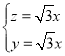 ,
,
令![]() ,从而
,从而![]() ,
,
而平面![]() 的法向量为
的法向量为![]() ,
,
故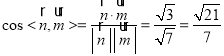 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为![]() 元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
序号 | 分组 | 频数(天) | 频率 |
1 |
|
| 0.16 |
2 |
| 12 |
|
3 |
|
| 0.3 |
4 |
|
|
|
5 |
| 5 | 0.1 |
合计 | 50 | 1 | |
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 关于日需求量
关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间![]() 内的概率.
内的概率.
【题目】为了保障某种药品的主要药理成分在国家药品监督管理局规定的值范围内,某制药厂在该药品的生产过程中,检验员在一天中按照规定每间隔2小时对该药品进行检测,每天检测4次:每次检测由检验员从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的其主要药理成分含量服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示某次抽取的20件产品中其主要药理成分含量在
表示某次抽取的20件产品中其主要药理成分含量在![]() 之外的药品件数,求
之外的药品件数,求![]() (精确到0.001)及
(精确到0.001)及![]() 的数学期望;
的数学期望;
(2)在一天内四次检测中,如果有一次出现了主要药理成分含量在![]() 之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查;如果在一天中,有连续两次检测出现了主要药理成分含量在
之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查;如果在一天中,有连续两次检测出现了主要药理成分含量在![]() 之外的药品,则需停止生产并对原材料进行检测.
之外的药品,则需停止生产并对原材料进行检测.
①下面是检验员在某一次抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() ,
,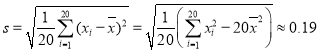 .其中
.其中![]() 为抽取的第
为抽取的第![]() 件药品的主要药理成分含量,
件药品的主要药理成分含量,![]() .用样本平均数
.用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
②试确定一天中需停止生产并对原材料进行检测的概率(精确到0.001).附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,
![]() .
.