题目内容
11.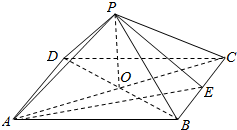 如图,在四棱锥P-ABCD中,底面是以O为中心的正方形,PO⊥底面ABCD,E为BC边的中点,PE⊥PA.
如图,在四棱锥P-ABCD中,底面是以O为中心的正方形,PO⊥底面ABCD,E为BC边的中点,PE⊥PA.(1)求证:平面PAE⊥平面PAD;
(2)求直线AC与平面PAD所成的角.
分析 (1)连接DE,证得△PDE≌△PAE,由线面垂直的判定和面面垂直的判定定理,即可得证;
(2)可设正方形的边长为2,PA=x,由线面垂直的性质和勾股定理,可得x,设C到平面PAD的距离为d,运用等积法,可得d,再由线面所成的角的正弦,可得所成的角.
解答  (1)证明:连接DE,
(1)证明:连接DE,
由DE=AE,PD=PA,PE=PE,
可得△PDE≌△PAE,
由PE⊥PA,可得PE⊥PD,
PA∩PD=P,
可得PE⊥平面PAD,
PE?平面PAE,
可得平面PAE⊥平面PAD;
(2)解:可设正方形的边长为2,PA=x,
则PE=$\sqrt{A{E}^{2}-P{A}^{2}}$=$\sqrt{5-{x}^{2}}$,
又PE=$\sqrt{P{B}^{2}-1}$=$\sqrt{{x}^{2}-1}$,
解得x=$\sqrt{3}$,
△PAD的面积为$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$,
设C到平面PAD的距离为d,
则VP-ACD=VC-PAD,
即有$\frac{1}{3}$×1×$\frac{1}{2}$×4=$\frac{1}{3}$×$\sqrt{2}$d,
解得d=$\sqrt{2}$,
又AC=2$\sqrt{2}$,
即有直线AC与平面PAD所成的角的正弦为$\frac{d}{AC}$=$\frac{1}{2}$,
则直线AC与平面PAD所成的角为30°.
点评 本题考查面面垂直的判定和直线和平面所成角的求法,考查空间直线和平面的位置关系,考查运算能力和推理能力,属于中档题.

练习册系列答案
相关题目
3.已知函数f(x)=|x|-1,若关于x的方程f2(x)+(2m-1)f(x)+4-2m=0有四个不同的实数解,则实数m的取值范围是( )
| A. | m<-2 | B. | m<-2.5 | C. | m<1.5 | D. | m>1.5 |
 在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,
在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,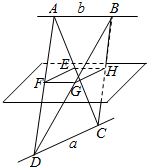 如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.
如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.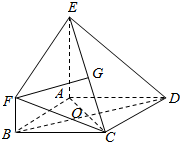 在如图所示的几何体中,底面ABCD是边长为2的菱形,∠ABC=60°,EA⊥平面ABCD,EA∥BF,EA=2BF=2,G为CE的中点,直线AC与BD相交于点O
在如图所示的几何体中,底面ABCD是边长为2的菱形,∠ABC=60°,EA⊥平面ABCD,EA∥BF,EA=2BF=2,G为CE的中点,直线AC与BD相交于点O