题目内容
1.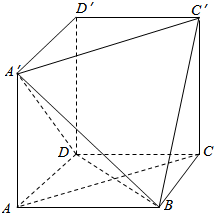 在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,
在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,(Ⅰ)若DD′=3,求几何体ABCD-A′C′D′的体积;
(Ⅱ)若DD′>1,且直线A′D与平面A′BC′所成的角的正弦值为$\frac{4\sqrt{5}}{15}$,求二面角D-A′B-C′的平面角的余弦值.
分析 (Ⅰ)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,利用向量法先求出${V}_{{B}^{'}-{A}^{'}B{C}^{'}}$,由此利用几何体ABCD-A′C′D′的体积:V=${V}_{长方体ABCD-{A}^{‘}{B}^{’}{C}^{‘}{D}^{’}}$-${V}_{{B}^{‘}-{A}^{’}B{C}^{‘}}$能求出结果.
(Ⅱ)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,由直线A′D与平面A′BC′所成的角的正弦值为$\frac{4\sqrt{5}}{15}$,求出DD′=4,由此利用向量法能求出二面角D-A′B-C′的平面角的余弦值.
解答 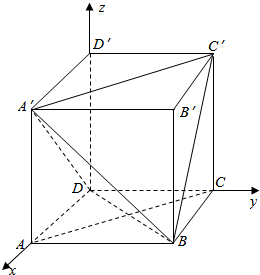 解:(Ⅰ)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,
解:(Ⅰ)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,
由已知得A′(2,0,3),B(2,2,0),B′(2,2,3),C′(0,2,3),
$\overrightarrow{{A}^{'}B}$=(0,2,-3),$\overrightarrow{{A}^{'}{B}^{'}}$=(0,2,0),$\overrightarrow{{A}^{'}{C}^{'}}$=(-2,2,0),
设平面A′BC′的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}^{'}B}=2y-3z=0}\\{\overrightarrow{n}•\overrightarrow{{A}^{'}{C}^{'}}=-2x+2y=0}\end{array}\right.$,取x=3,得$\overrightarrow{n}$=(3,3,2),
∴B′到平面A′BC′的距离h=$\frac{|\overrightarrow{{A}^{'}{B}^{'}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{6}{\sqrt{22}}$,
cos<$\overrightarrow{{A}^{'}B},\overrightarrow{{A}^{'}{C}^{'}}$>=$\frac{\overrightarrow{{A}^{'}B}•\overrightarrow{{A}^{'}{C}^{'}}}{|\overrightarrow{{A}^{'}B}|•|\overrightarrow{{A}^{'}{C}^{'}}|}$=$\frac{4}{\sqrt{13}•\sqrt{8}}$=$\frac{2}{\sqrt{26}}$.
∴sin∠BA′C′=$\sqrt{1-(\frac{2}{\sqrt{26}})^{2}}$=$\frac{22}{\sqrt{26}}$,
∴${S}_{△{A}^{'}B{C}^{'}}$=$\frac{1}{2}|\overrightarrow{{A}^{'}B}|•|\overrightarrow{{A}^{'}{C}^{'}}|$sin∠BA′C′=$\frac{1}{2}×\sqrt{13}×\sqrt{8}×\frac{22}{\sqrt{26}}$=22,
∴${V}_{{B}^{'}-{A}^{'}B{C}^{'}}$=$\frac{1}{3}h{S}_{△{A}^{'}B{C}^{'}}$=$\frac{1}{3}×\frac{6}{\sqrt{22}}×22$=2$\sqrt{22}$,
∴几何体ABCD-A′C′D′的体积:
V=${V}_{长方体ABCD-{A}^{‘}{B}^{’}{C}^{‘}{D}^{’}}$-${V}_{{B}^{‘}-{A}^{’}B{C}^{‘}}$
=$2×2×3-2\sqrt{22}$
=12-2$\sqrt{22}$.
(Ⅱ)以D为原点,DA为x轴,DC为y轴,DD′为z轴,建立空间直角坐标系,
设DD′=t(t>1),则A′(2,0,t),B(2,2,0),B′(2,2,t),C′(0,2,t),
$\overrightarrow{{A}^{'}B}$=(0,2,-t),$\overrightarrow{{A}^{'}{B}^{'}}$=(0,2,0),$\overrightarrow{{A}^{'}{C}^{'}}$=(-2,2,0),$\overrightarrow{D{A}^{'}}$=(2,0,t),
设平面A′BC′的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}^{'}B}=2y-tz=0}\\{\overrightarrow{n}•\overrightarrow{{A}^{'}{C}^{'}}=-2x+2y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,1,$\frac{2}{t}$),
∵直线A′D与平面A′BC′所成的角的正弦值为$\frac{4\sqrt{5}}{15}$,
∴cos<$\overrightarrow{D{A}^{'}}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{D{A}^{'}}•\overrightarrow{n}}{|\overrightarrow{D{A}^{'}}|•|\overrightarrow{n}|}$=$\frac{4}{\sqrt{4+{t}^{2}}•\sqrt{1+1+\frac{4}{{t}^{2}}}}$=$\frac{4\sqrt{5}}{15}$,
由t>1,解得t=4,
∴$\overrightarrow{n}$=(1,1,$\frac{1}{2}$),$\overrightarrow{D{A}^{'}}$=(2,0,4),$\overrightarrow{DB}$=(2,2,0),
设平面DA′B的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{D{A}^{'}}=2a+4c=0}\\{\overrightarrow{m}•\overrightarrow{DB}=2a+2b=0}\end{array}\right.$,取a=2,得$\overrightarrow{m}$=(2,-2,-1),
设二面角D-A′B-C′的平面角为θ,
则cosθ=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{2-2-\frac{1}{2}}{\sqrt{\frac{9}{4}}•\sqrt{9}}$|=$\frac{1}{9}$.
∴二面角D-A′B-C′的平面角的余弦值为$\frac{1}{9}$.
点评 本题考查几何体的体积的求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案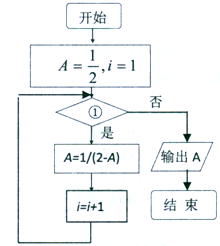 如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )
如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
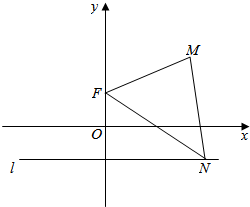 如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.
如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.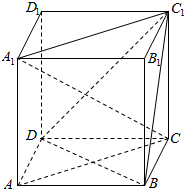 如图,在边长为1的正方体ABCD-A1B1C1D1中,求证:
如图,在边长为1的正方体ABCD-A1B1C1D1中,求证: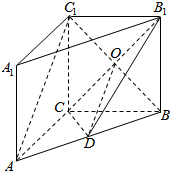 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.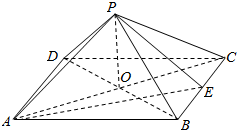 如图,在四棱锥P-ABCD中,底面是以O为中心的正方形,PO⊥底面ABCD,E为BC边的中点,PE⊥PA.
如图,在四棱锥P-ABCD中,底面是以O为中心的正方形,PO⊥底面ABCD,E为BC边的中点,PE⊥PA.