题目内容
1．已知：log310=a，log625=b，求log445．分析 利用换底公式转化已知条件为log23，log25的方程，求出两个值，化简所求表达式，代入求解即可．
解答 解：log310=log32+log35=a，…①，
log310=$\frac{1+{log}_{2}5}{{log}_{2}3}$=a，…②
log625=b，可得$\frac{2{log}_{2}5}{1+{log}_{2}3}=b$…③，
解②③可得${log}_{2}3=\frac{2+b}{2a-b}$，代入①，可得${log}_{2}5=\frac{2b（a+1）}{2a-b}$，
log445=$\frac{1}{2}$log2（5×9）=$\frac{1}{2}$log25+log23=$\frac{b（a+1）}{2a-b}$$+\frac{2+b}{2a-b}$=$\frac{ab+2+2b}{2a-b}$．
点评 本题考查对数的换底公式以及化简求值，考查函数与方程的思想，是基础题．
练习册系列答案
相关题目
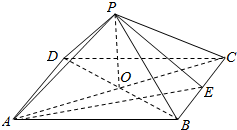如图，在四棱锥P-ABCD中，底面是以O为中心的正方形，PO⊥底面ABCD，E为BC边的中点，PE⊥PA．
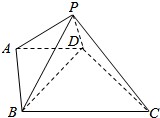直角梯形ABCD中，∠ABC=90°，AB=AD=AP=1，BC=2，平面ABP垂直于底面ABCD．
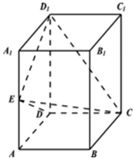（Ⅰ）证明：A1B1∥平面CDE；