题目内容
给定两个命题,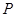 :对任意实数
:对任意实数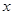 都有
都有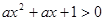 恒成立;
恒成立;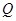 :
: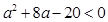 .如果
.如果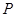 ∨
∨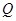 为真命题,
为真命题,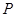 ∧
∧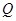 为假命题,求实数
为假命题,求实数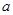 的取值范围.
的取值范围.
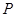 :对任意实数
:对任意实数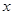 都有
都有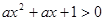 恒成立;
恒成立;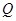 :
: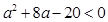 .如果
.如果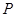 ∨
∨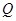 为真命题,
为真命题,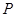 ∧
∧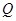 为假命题,求实数
为假命题,求实数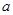 的取值范围.
的取值范围.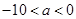 或
或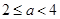 .
.试题分析:先分别求出
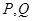 为真时
为真时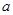 的取值范围,对命题
的取值范围,对命题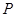 :
: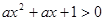 恒成立,先检验
恒成立,先检验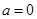 时是否符合要求,当
时是否符合要求,当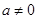 时,由
时,由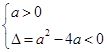 求解即可,从而得到
求解即可,从而得到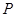 真时
真时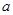 的取值范围;对命题
的取值范围;对命题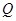 :
: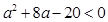 ,求得
,求得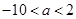 , 由
, 由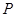 ∨
∨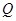 为真命题,
为真命题,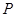 ∧
∧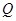 为假命题,结合复合命题的真值表可知
为假命题,结合复合命题的真值表可知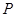 ,
,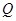 中有且只有一个为真,分别求出
中有且只有一个为真,分别求出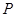 真
真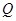 假时与
假时与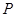 假
假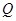 真时
真时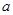 的取值范围,取两种情况的并集即可确定
的取值范围,取两种情况的并集即可确定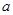 的取值范围.
的取值范围.试题解析:命题
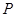 :
: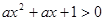 恒成立
恒成立当
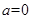 时,不等式恒成立,满足题意 2分
时,不等式恒成立,满足题意 2分当
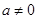 时,
时,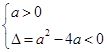 ,解得
,解得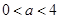 4分
4分∴
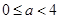 6分
6分命题
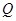 :
: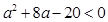 解得
解得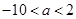 9分
9分∵
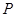 ∨
∨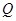 为真命题,
为真命题,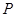 ∧
∧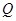 为假命题
为假命题∴
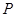 ,
,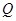 有且只有一个为真 11分
有且只有一个为真 11分如图可得

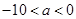 或
或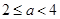 13分.
13分.
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
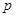 : 关于
: 关于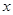 的不等式
的不等式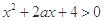 ,对一切
,对一切 恒成立; 命题
恒成立; 命题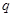 : 函数
: 函数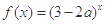 在
在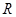 上是增函数.若
上是增函数.若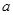 的取值范围.
的取值范围.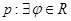 ,使
,使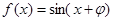 为偶函数;命题
为偶函数;命题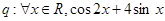
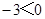 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )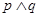


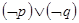
 p:?x∈R,sinx>1
p:?x∈R,sinx>1 ”的必要不充分条件
”的必要不充分条件 ,0)为函数f(x)=tan(2x+
,0)为函数f(x)=tan(2x+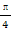 )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则(
)的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则(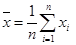 ,
,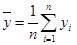 ,则回归直线y=bx+a必过点(
,则回归直线y=bx+a必过点(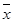 ,
, 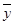 ).
).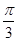 个单位,得到函数y=sin
个单位,得到函数y=sin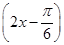 的图象;
的图象;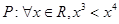 ,命题
,命题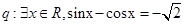 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )