题目内容
12.已知函数y=x2+x-1,求:(1)x∈[-1,2]的值域;
(2)x∈[1,3]的值域.
分析 根据二次函数的单调性质即可求出答案.
解答 解:(1)函数y=x2+x-1的对称轴为x=-$\frac{1}{2}$,图象的开口向上,
∴函数[-1,-$\frac{1}{2}$)上单调递减,在(-$\frac{1}{2}$,2]上单调递增,
∴当x=-$\frac{1}{2}$,函数有最小值,y=$\frac{1}{4}$-$\frac{1}{2}$-1=-$\frac{5}{4}$,
当x=2,函数有最大值,y=4+2-1=5,
∴x∈[-1,2]的值域为[-$\frac{5}{4}$,5];
(2)由(1)知,函数在[1,3]单调递增,
∴当x=1,函数有最小值,y=1+1-1=1,
当x=3,函数有最大值,y=9+3-1=11,
∴x∈[1,3]的值域为[1,11].
点评 本题考查了根据二次函数的图象和性质求函数的值域的方法,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.函数y=$\frac{1}{lo{g}_{2}x-2}$的定义域为 ( )
| A. | (0,4) | B. | (4,+∞) | C. | (0,4)∪(4,+∞) | D. | (0,+∞) |
2.下列四个图形中,是函数图象的有( )
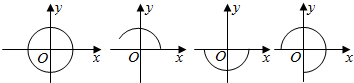

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
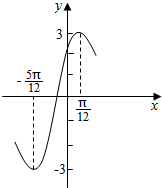 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.