题目内容
2.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:f′(x)是函数f(x)的导函数,f″(x)是f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$,根据这一发现,可求得f($\frac{1}{2016}$)+f($\frac{2}{2016}$)+…+f($\frac{2015}{2016}$)=2015.分析 根据函数f(x)的解析式求出f′(x)和f″(x),令f″(x)=0,求得x的值,由此求得函数f(x)的对称中心,得到f(1-x)+f(x)=2,即可得出.
解答 解:依题意,得:f′(x)=x2-x+3,∴f″(x)=2x-1.
由f″(x)=0,即2x-1=0.
∴x=$\frac{1}{2}$,
∴f($\frac{1}{2}$)=1,
∴f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$的对称中心为($\frac{1}{2}$,1)
∴f(1-x)+f(x)=2,
∴f($\frac{1}{2016}$)+f($\frac{2}{2016}$)+…+f($\frac{2015}{2016}$)=2015,
故答案为:2015.
点评 本题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,函数的对称性的应用,属于中档题.

练习册系列答案
相关题目
10.实数x,y满足x2+y2-2x-2y+1=0,则$\frac{y-4}{x-2}$的最小值为( )
| A. | $-\frac{3}{4}$ | B. | $-\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
11.已知函数y=f(-|x|)的图象如左图所示,则函数y=f(x)的图象不可能是( )

| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
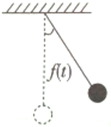 一个单摆如图所示,角(弧度)从竖直开始移动作为时间(秒)的函数满足f(x)=$\frac{1}{2}$sin(2t+$\frac{π}{2}$).求:多长时间单摆完成5次完整摆动?
一个单摆如图所示,角(弧度)从竖直开始移动作为时间(秒)的函数满足f(x)=$\frac{1}{2}$sin(2t+$\frac{π}{2}$).求:多长时间单摆完成5次完整摆动?