题目内容
在数列{an}中,a1=1,an+1=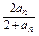 ,n∈N*,猜想这个数列的通项公式是什么?这个猜想正确吗?说明理由.
,n∈N*,猜想这个数列的通项公式是什么?这个猜想正确吗?说明理由.
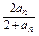 ,n∈N*,猜想这个数列的通项公式是什么?这个猜想正确吗?说明理由.
,n∈N*,猜想这个数列的通项公式是什么?这个猜想正确吗?说明理由.{an}的通项公式an=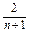
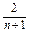
在{an}中,a1=1,a2=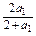 =
=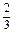 ,
,
a3=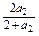 =
=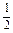 =
=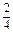 ,a4=
,a4=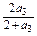 =
=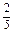 ,…,
,…,
所以猜想{an}的通项公式an=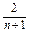 .
.
这个猜想是正确的.
证明如下:因为a1=1,an+1=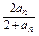 ,
,
所以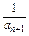 =
=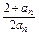 =
=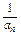 +
+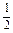 ,即
,即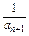 -
-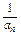 =
=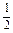 ,
,
所以数列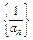 是以
是以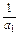 =1为首项,
=1为首项,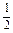 为公差的等差数列,
为公差的等差数列,
所以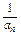 =1+
=1+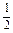 (n-1)=
(n-1)= 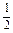 n+
n+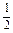 ,
,
所以通项公式an=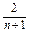 .
.
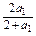 =
=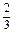 ,
,a3=
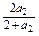 =
=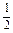 =
=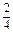 ,a4=
,a4=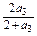 =
=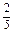 ,…,
,…,所以猜想{an}的通项公式an=
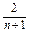 .
.这个猜想是正确的.
证明如下:因为a1=1,an+1=
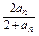 ,
,所以
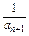 =
=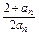 =
=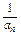 +
+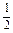 ,即
,即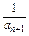 -
-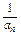 =
=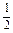 ,
,所以数列
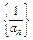 是以
是以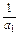 =1为首项,
=1为首项,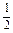 为公差的等差数列,
为公差的等差数列,所以
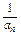 =1+
=1+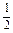 (n-1)=
(n-1)= 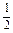 n+
n+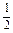 ,
,所以通项公式an=
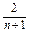 .
.
练习册系列答案
相关题目
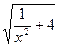 (x>0),数列{an}中,a1=1,
(x>0),数列{an}中,a1=1,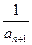 =-f(an),求数列{an}的通项公式.
=-f(an),求数列{an}的通项公式.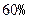 (即衰变了
(即衰变了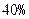 ),该动物大约在距今多少年前死亡?
),该动物大约在距今多少年前死亡?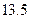 万元的新车,专家预测这种车每年按
万元的新车,专家预测这种车每年按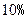 的速度折旧.
的速度折旧.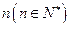 年后这辆车的价值.
年后这辆车的价值.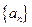 中,
中,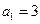 ,
,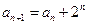 ,求
,求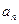 .
.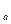 !=(n
!=(n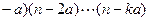 ,其中k是满足n>ka的最大整数,那么
,其中k是满足n>ka的最大整数,那么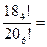 _________
_________