题目内容
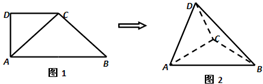 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=2,AD=CD=1.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.求几何体D-ABC的体积.
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=2,AD=CD=1.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.求几何体D-ABC的体积.分析:取AC中点O,连接DO,则OD⊥平面ABC,再利用三棱锥体积公式,即可求得结论.
解答: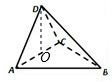 解:取AC中点O,连接DO,则DO⊥AC,
解:取AC中点O,连接DO,则DO⊥AC,
∵面ADC⊥面ABC,面ADC∩面ABC=AC,DO?面ACD,
∴OD⊥平面ABC,…(3分)
∴OD为三棱锥D-ABC的高,OD=
.…(4分)
在图1中,可得AC=BC=
,从而AC2+BC2=AB2,故AC⊥BC,S△ABC=1.…(6分)
∴VD-ABC=
Sh=
×1×
=
…(8分)
 解:取AC中点O,连接DO,则DO⊥AC,
解:取AC中点O,连接DO,则DO⊥AC,∵面ADC⊥面ABC,面ADC∩面ABC=AC,DO?面ACD,
∴OD⊥平面ABC,…(3分)
∴OD为三棱锥D-ABC的高,OD=
| ||
| 2 |
在图1中,可得AC=BC=
| 2 |
∴VD-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
点评:本题考查三棱锥体积的计算,考查学生的计算能力,正确求三棱锥的高是关键.

练习册系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.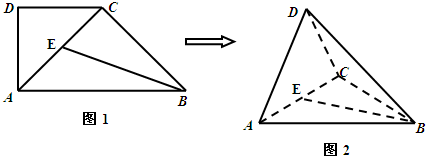 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;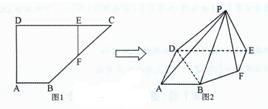 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.