题目内容
(2013•肇庆二模)如图1,在直角梯形ABCD中,已知AD∥BC,AD=AB=1,∠BAD=90°,∠BCD=45°,AE⊥BD.将△ABD沿对角线BD折起(图2),记折起后点A的位置为P且使平面PBD⊥平面BCD.
(1)求三棱锥P-BCD的体积;
(2)求平面PBC与平面PCD所成二面角的平面角的大小.

(1)求三棱锥P-BCD的体积;
(2)求平面PBC与平面PCD所成二面角的平面角的大小.

分析:(1)由题意证明PE为三棱锥P-BCD的高,由原图形可得三角形BDC为等腰直角三角形,求出其面积,则三棱锥P-BCD的体积可求;
(2)由(1)的求解过程知道PE⊥BD,DC⊥BD,过E作DC的平行线后以E点为坐标原点建立空间直角坐标系,求出平面PBC与平面PCD的法向量,由平面法向量求平面PBC与平面PCD所成二面角的平面角的大小.
(2)由(1)的求解过程知道PE⊥BD,DC⊥BD,过E作DC的平行线后以E点为坐标原点建立空间直角坐标系,求出平面PBC与平面PCD的法向量,由平面法向量求平面PBC与平面PCD所成二面角的平面角的大小.
解答:解:(1)∵平面PBD⊥平面BCD,PE⊥BD,PE?平面PBD,平面PBD∩平面BCD=BD,
∴PE⊥平面BCD,
即PE是三棱锥P-BCD的高,
又∵AD∥BC,AD=AB=1,∠BAD=90°,∠BCD=45°,
∴∠ABD=∠CBD=45°,∠BDC=90°,CD=BD=
=
,
∴PE=AE=ABsin45o=
,S△BCD=
BD•CD=
×
×
=1,
∴三棱锥P-BCD的体积V=
S△BCD•PE=
×1×
=
.
(2)过E作直线EG∥DC,交BC于G,则EG⊥BD,EG⊥PE
如图建立空间直角坐标系,
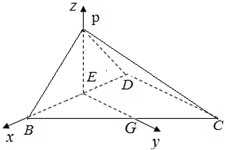
则P(0,0,
),B(
,0,0),C(-
,
,0),D(-
,0,0).
=(
,0,-
),
=(-
,
,-
),
=(-
,0,-
).
设平面PBC的法向量为
=(x,y,z),
则
,即
,化简得
令x=1,得z=1,y=1,所以
=(1,1,1)是平面PBC的一个法向量.
再设
=(x1,y1,z1),
则
,即
,化简得
令x1=1,得y1=0,z1=-1,所以平面PCD的一个法向量为
=(1,0,-1).
设向量
和
所成角为θ,则cosθ=|
|=
=0.
∴平面PBC与平面PCD所成二面角的平面角的大小为90°.
∴PE⊥平面BCD,
即PE是三棱锥P-BCD的高,
又∵AD∥BC,AD=AB=1,∠BAD=90°,∠BCD=45°,
∴∠ABD=∠CBD=45°,∠BDC=90°,CD=BD=
| AB2+AD2 |
| 2 |
∴PE=AE=ABsin45o=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴三棱锥P-BCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
(2)过E作直线EG∥DC,交BC于G,则EG⊥BD,EG⊥PE
如图建立空间直角坐标系,

则P(0,0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| PB |
| ||
| 2 |
| ||
| 2 |
| PC |
| ||
| 2 |
| 2 |
| ||
| 2 |
| PD |
| ||
| 2 |
| ||
| 2 |
设平面PBC的法向量为
| n |
则
|
|
|
令x=1,得z=1,y=1,所以
| n |
再设
| m |
则
|
|
|
令x1=1,得y1=0,z1=-1,所以平面PCD的一个法向量为
| m |
设向量
| n |
| m |
| ||||
|
|
| 0 | ||||
|
∴平面PBC与平面PCD所成二面角的平面角的大小为90°.
点评:本题考查了棱锥的体积的求法,考查了二面角的平面角及求法,综合考查了学生的空间想象能力和思维能力,解答此题时一定要注意折叠前后的变量与不变量,此题是中档题.

练习册系列答案
相关题目