╠Ō─┐─┌╚▌
 Ż©2013•║ŻĄĒŪ°Č■─ŻŻ®╚ń═╝1Ż¼į┌ų▒ĮŪ╠▌ą╬ABCDųąŻ¼ĪŽABC=ĪŽDAB=90ĪŃŻ¼ĪŽCAB=30ĪŃŻ¼BC=2Ż¼AD=4Ż«░čĪ„DACčžČįĮŪŽ▀ACš█ŲĄĮĪ„PACĄ─╬╗ų├Ż¼╚ń═╝2╦∙╩ŠŻ¼╩╣Ą├ĄŃPį┌ŲĮ├µABC╔ŽĄ─š²═Čė░HŪĪ║├┬õį┌Ž▀Č╬AC╔ŽŻ¼┴¼ĮėPBŻ¼ĄŃEŻ¼FĘų▒╬¬Ž▀Č╬PAŻ¼PBĄ─ųąĄŃŻ«
Ż©2013•║ŻĄĒŪ°Č■─ŻŻ®╚ń═╝1Ż¼į┌ų▒ĮŪ╠▌ą╬ABCDųąŻ¼ĪŽABC=ĪŽDAB=90ĪŃŻ¼ĪŽCAB=30ĪŃŻ¼BC=2Ż¼AD=4Ż«░čĪ„DACčžČįĮŪŽ▀ACš█ŲĄĮĪ„PACĄ─╬╗ų├Ż¼╚ń═╝2╦∙╩ŠŻ¼╩╣Ą├ĄŃPį┌ŲĮ├µABC╔ŽĄ─š²═Čė░HŪĪ║├┬õį┌Ž▀Č╬AC╔ŽŻ¼┴¼ĮėPBŻ¼ĄŃEŻ¼FĘų▒╬¬Ž▀Č╬PAŻ¼PBĄ─ųąĄŃŻ«Ż©ó±Ż®Ū¾ųżŻ║ŲĮ├µEFHĪ╬ŲĮ├µPBCŻ╗
Ż©ó“Ż®Ū¾ų▒Ž▀HEėļŲĮ├µPHB╦∙│╔ĮŪĄ─š²ŽęųĄŻ╗
Ż©ó¾Ż®į┌└ŌPA╔Ž╩Ūʱ┤µį┌ę╗ĄŃMŻ¼╩╣Ą├MĄĮPŻ¼HŻ¼AŻ¼F╦─ĄŃĄ─ŠÓ└ļŽÓĄ╚Ż┐Ūļ╦Ą├„└Ēė╔Ż«
Ęų╬÷Ż║Ż©ó±Ż®ę└╠ŌęŌŻ¼┐╔ųżĄ├Ī„ADCŻ©╝┤Ī„PDCŻ®╩ŪĄ╚▒▀╚²ĮŪą╬⇒H╩ŪACĄ─ųąĄŃŻ¼┤ėČ°┐╔ų¬HEĪ╬PCŻ¼┐╔ų¬═¼└ĒEFĪ╬PBŻ¼└¹ė├├µ├µŲĮąąĄ─┼ąČŽČ©└Ē╝┤┐╔ųżĄ├Įß┬█Ż╗
Ż©ó“Ż®į┌ŲĮ├µABC─┌╣²Hū„ACĄ─┤╣Ž▀Ż¼ęįH╬¬ū°▒ĻįŁĄŃĮ©┴ó┐š╝õų▒ĮŪū°▒ĻŽĄŻ¼╝╠Č°┐╔Ū¾Ą├AŻ¼PŻ¼BŻ¼EĄ─ū°▒ĻŻ¼╔ĶŲĮ├µPHBĄ─Ę©Ž“┴┐
=Ż©xŻ¼yŻ¼zŻ®Ż¼ė╔
┐╔Ū¾Ą├
Ż¼═©╣²ČįxĖ│ųĄŻ¼┐╔Ū¾Ą├
=Ż©
Ż¼-3Ż¼0Ż®Ż¼└¹ė├Ž“┴┐Ą─╩²┴┐╗²╝┤┐╔Ū¾Ą├cosŻ╝
Ż¼
ŻŠŻ¼╝┤HEėļŲĮ├µPHB╦∙│╔ĮŪĄ─š²ŽęųĄŻ╗
Ż©ó¾Ż®į┌ų▒ĮŪ╚²ĮŪą╬PHAųąŻ¼EH=PE=EA=
PA=2Ż¼į┌ų▒ĮŪ╚²ĮŪą╬PHBųąŻ¼PB=4Ż¼EF=
PB=2Ż¼┤ėČ°┐╔ų¬E╬¬M╝┤┐╔Ż«
Ż©ó“Ż®į┌ŲĮ├µABC─┌╣²Hū„ACĄ─┤╣Ž▀Ż¼ęįH╬¬ū°▒ĻįŁĄŃĮ©┴ó┐š╝õų▒ĮŪū°▒ĻŽĄŻ¼╝╠Č°┐╔Ū¾Ą├AŻ¼PŻ¼BŻ¼EĄ─ū°▒ĻŻ¼╔ĶŲĮ├µPHBĄ─Ę©Ž“┴┐
| n |
|
|
| n |
| 3 |
| n |
| HE |
Ż©ó¾Ż®į┌ų▒ĮŪ╚²ĮŪą╬PHAųąŻ¼EH=PE=EA=
| 1 |
| 2 |
| 1 |
| 2 |
ĮŌ┤Ż║ĮŌŻ║Ż©ó±Ż®Ī▀ĄŃPį┌ŲĮ├µABC╔ŽĄ─š²═Čė░HŪĪ║├┬õį┌Ž▀Č╬AC╔ŽŻ¼
╦∙ęįPHĪ═ŲĮ├µABCŻ¼╦∙ęįPHĪ═ACŻ¼ĪŁ1Ęų
Ī▀į┌ų▒ĮŪ╠▌ą╬ABCDųąŻ¼ĪŽABC=ĪŽDAB=90ĪŃŻ¼ĪŽCAB=30ĪŃŻ¼BC=2Ż¼AD=4Ż¼
ĪÓAC=4Ż¼ĪŽCAB=60ĪŃŻ¼
ĪÓĪ„ADC╩ŪĄ╚▒▀╚²ĮŪą╬Ż¼╣╩H╩ŪACĄ─ųąĄŃŻ¼ĪŁ2Ęų
ĪÓHEĪ╬PCĪŁ3Ęų
═¼└Ē┐╔ųżEFĪ╬PBŻ¼
ėųHEĪ╔EF=EŻ¼CPĪ╔PB=PŻ¼
ĪÓŲĮ├µEFHĪ╬ŲĮ├µPBCŻ╗ĪŁ5Ęų
Ż©ó“Ż®į┌ŲĮ├µABC─┌╣²Hū„ACĄ─┤╣Ž▀Ż¼╚ń═╝Į©┴ó┐š╝õų▒ĮŪū°▒ĻŽĄŻ¼į“AŻ©0Ż¼-2Ż¼0Ż®Ż¼PŻ©0Ż¼0Ż¼2
Ż®Ż¼BŻ©
Ż¼1Ż¼0Ż®ĪŁ6Ęų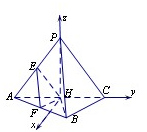
ę“╬¬EŻ©0Ż¼-1Ż¼
Ż®Ż¼
=Ż©0Ż¼-1Ż¼
Ż®Ż¼╔ĶŲĮ├µPHBĄ─Ę©Ž“┴┐
=Ż©xŻ¼yŻ¼zŻ®Ż¼
Ī▀
=Ż©
Ż¼1Ż¼0Ż®Ż¼
=Ż©0Ż¼0Ż¼2
Ż®Ż¼
ĪÓ
Ż¼╝┤
Ż¼
┴Ņx=
Ż¼į“y=-3Ż¼
ĪÓ
=Ż©
Ż¼-3Ż¼0Ż®ĪŁ8Ęų
cosŻ╝
Ż¼
ŻŠ=
=
=
ĪŁ10Ęų
ĪÓų▒Ž▀HEėļŲĮ├µPHB╦∙│╔ĮŪĄ─š²ŽęųĄ╬¬
ĪŁ11Ęų
Ż©ó¾Ż®┤µį┌Ż¼╩┬╩Ą╔Ž╝ŪĄŃE╬¬M╝┤┐╔ĪŁ12Ęų
ę“╬¬į┌ų▒ĮŪ╚²ĮŪą╬PHAųąŻ¼EH=PE=EA=
PA=2ĪŁ13Ęų
į┌ų▒ĮŪ╚²ĮŪą╬PHBųąŻ¼PB=4Ż¼EF=
PB=2Ż¼
╦∙ęįĄŃEĄĮPŻ¼HŻ¼AŻ¼F╦─ĄŃĄ─ŠÓ└ļŽÓĄ╚ĪŁ14Ęų
╦∙ęįPHĪ═ŲĮ├µABCŻ¼╦∙ęįPHĪ═ACŻ¼ĪŁ1Ęų
Ī▀į┌ų▒ĮŪ╠▌ą╬ABCDųąŻ¼ĪŽABC=ĪŽDAB=90ĪŃŻ¼ĪŽCAB=30ĪŃŻ¼BC=2Ż¼AD=4Ż¼
ĪÓAC=4Ż¼ĪŽCAB=60ĪŃŻ¼
ĪÓĪ„ADC╩ŪĄ╚▒▀╚²ĮŪą╬Ż¼╣╩H╩ŪACĄ─ųąĄŃŻ¼ĪŁ2Ęų
ĪÓHEĪ╬PCĪŁ3Ęų
═¼└Ē┐╔ųżEFĪ╬PBŻ¼
ėųHEĪ╔EF=EŻ¼CPĪ╔PB=PŻ¼
ĪÓŲĮ├µEFHĪ╬ŲĮ├µPBCŻ╗ĪŁ5Ęų
Ż©ó“Ż®į┌ŲĮ├µABC─┌╣²Hū„ACĄ─┤╣Ž▀Ż¼╚ń═╝Į©┴ó┐š╝õų▒ĮŪū°▒ĻŽĄŻ¼į“AŻ©0Ż¼-2Ż¼0Ż®Ż¼PŻ©0Ż¼0Ż¼2
| 3 |
| 3 |

ę“╬¬EŻ©0Ż¼-1Ż¼
| 3 |
| HE |
| 3 |
| n |
Ī▀
| HB |
| 3 |
| HP |
| 3 |
ĪÓ
|
|
┴Ņx=
| 3 |
ĪÓ
| n |
| 3 |
cosŻ╝
| n |
| HE |
| ||||
|
|
| 3 | ||
2Ī┴2
|
| ||
| 4 |
ĪÓų▒Ž▀HEėļŲĮ├µPHB╦∙│╔ĮŪĄ─š²ŽęųĄ╬¬
| ||
| 4 |
Ż©ó¾Ż®┤µį┌Ż¼╩┬╩Ą╔Ž╝ŪĄŃE╬¬M╝┤┐╔ĪŁ12Ęų
ę“╬¬į┌ų▒ĮŪ╚²ĮŪą╬PHAųąŻ¼EH=PE=EA=
| 1 |
| 2 |
į┌ų▒ĮŪ╚²ĮŪą╬PHBųąŻ¼PB=4Ż¼EF=
| 1 |
| 2 |
╦∙ęįĄŃEĄĮPŻ¼HŻ¼AŻ¼F╦─ĄŃĄ─ŠÓ└ļŽÓĄ╚ĪŁ14Ęų
ĄŃŲ└Ż║▒Š╠Ō┐╝▓ķŲĮ├µėļŲĮ├µŲĮąąĄ─┼ąČ©Ż¼┐╝▓ķų▒Ž▀ėļŲĮ├µ╦∙│╔Ą─ĮŪŻ¼┐╝▓ķĄŃĪóŽ▀Īó├µ╝õĄ─ŠÓ└ļ╝Ų╦ŃŻ¼═╗│÷┐╝▓ķ┐š╝õŽ“┴┐į┌┐š╝õ╝Ė║╬ųąĄ─ė”ė├Ż¼┐╝▓ķ┬▀╝Ł═Ų└Ēėļųż├„Ą──▄┴”Ż¼╩¶ė┌─č╠ŌŻ«

┴ĘŽ░▓ߎĄ┴ą┤░Ė
ŽÓ╣ž╠Ō─┐