题目内容
16.已知方程x2+2kx+k2=x,求使方程有两个大于1的实数根的充要条件,并写出它的一个必要不充分条件.分析 先写出使两根都大于1的充要条件是使两根都大于1的充要条件是:$\left\{\begin{array}{l}{(2k-1)^{2}-4{k}^{2}≥0}\\{({x}_{1}-1)+({x}_{2}-1)>0}\\{({x}_{1}-1)({x}_{2}-1)>0}\end{array}\right.$;再结合韦达定理解不等式即可得到结论.
解答 解:方程x2+2kx+k2=x,即方程x2+(2k-1)x+k2=0,
设方程的两根为x1,x2,
∴x1+x2=1-2k,x1•x2=k2,
则使两根都大于1的充要条件是:$\left\{\begin{array}{l}{(2k-1)^{2}-4{k}^{2}≥0}\\{({x}_{1}-1)+({x}_{2}-1)>0}\\{({x}_{1}-1)({x}_{2}-1)>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{4k-1≤0}\\{1-2k-2≤0}\\{{k}^{2}-1+2k+1≥0}\end{array}\right.$,
解得k≤-2,
所以方程x2+(k-2)x+k2+1=0有两个大于1的根的充要条件是k≤-2,
它的一个必要不充分条件是k≤-3.
点评 本题主要考查一元二次方程的根的分布与系数的关系.解决这一类型题目一般都要结合韦达定理,以及充要条件和必要条件的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列说法中正确的是( )
| A. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2],有(x2+2x)min≥(ax)max” | |
| D. | 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
6.在平行四边形ABCD中,AC与BD交于点O,E是OB的中点,若$\overrightarrow{AC}$=$\overrightarrow a$,$\overrightarrow{BD}$=$\overrightarrow b$,则$\overrightarrow{CE}$等于( )
| A. | -$\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$ | C. | $\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$ | D. | -$\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$ |
 ,若
,若 ,则实数
,则实数 的值是____________.
的值是____________.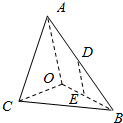 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.