题目内容
1.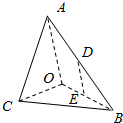 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.(1)求证:CO⊥平面AOB;
(2)在线段CB上是否存在一点F,使得平面DEF∥平面AOC,若存在,试确定F的位置;若不存在,请说明理由.
分析 (1)欲证平面COD⊥平面AOB,根据面面垂直的判定定理可知在平面COD内一直线与平面AOB垂直,根据勾股定理可知OC⊥OB,根据线面垂直的判定定理可知OC⊥平面AOB,
(2)取CB的中点F,连接DF,EF,则DF∥AC,DE∥AO,从而可得平面DEF∥平面AOC.
解答  (1)证明:∵AO⊥底面BOC,
(1)证明:∵AO⊥底面BOC,
∴AO⊥OC,AO⊥OB.
∵∠OAB=∠OAC=30°,AB=AC=2,
∴OC=OB=1.
∵BC=$\sqrt{2}$,由勾股定理得OC⊥OB,
∴OC⊥平面AOB.
(2)存在CB的中点F满足题意,
证明:取CB的中点F,连接DF,EF,则由于D,E分别为AB,OB的中点,有DF∥AC,DE∥AO,
∵DF∩DE=D,AC∩AO=A,DF,DE?平面DEF,AO,AC?平面AOC,
∴平面DEF∥平面AOC.
点评 本题主要考查了直线与平面垂直的判定,平面与平面平行的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
相关题目
9.已知中心在原点的双曲线C的右焦点为F(4,0),离心率等于$\frac{4}{3}$,则C的方程是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{25}$=1 |
 中,有一个内角为30°,“
中,有一个内角为30°,“ ”是“
”是“ ”的( )条件.
”的( )条件.