题目内容
4.已知函数f(x)=2x+x,g(x)=x-log${\;}_{\frac{1}{2}}$x,h(x)=log2x-$\sqrt{x}$的零点分别为x1,x2 ,x3,则x1,x2 ,x3的大小关系是x1<x2<x3.分析 根据函数解析式判断出f(x)=2x+x,g(x)=x-log${\;}_{\frac{1}{2}}$x,h(x)=log2x-$\sqrt{x}$都是单调递增函数,运用函数零点定理判断x1,x2 ,x3的范围即可得x1,x2 ,x3的大小
解答 解:∵f(x)=2x+x,g(x)=x-log${\;}_{\frac{1}{2}}$x,h(x)=log2x-$\sqrt{x}$都是单调递增函数,
∴f(x)=2x+x,g(x)=x-log${\;}_{\frac{1}{2}}$x,h(x)=log2x-$\sqrt{x}$均只有一个零点,
∵f(-1)=$\frac{1}{2}$-1=-$\frac{1}{2}$<0,f(0)=1>0,
∴f(x)=2x+x的零点x1∈(-1,0).
∵$\lim_{x→0}$g(x)=-∞,g(1)=1>0
∴g(x)的零点x2∈(0,1);
∵h(4)=0
∴h(x)的零点x3=4,
∴x1<x2<x3.
故答案为:x1<x2<x3
点评 本题考查了函数的单调性,在求解函数零点的范围问题中的应用,结合函数零点定理判断即可.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
19.如果事件A,B互斥,记$\overline{A}$,$\overline{B}$分别为事件A,B的对立事件,那么( )
| A. | A∪B是必然事件 | B. | $\overline{A}$∪$\overline{B}$是必然事件 | C. | $\overline{A}$与$\overline{B}$一定互斥 | D. | $\overline{A}$与$\overline{B}$一定不互斥 |
9.已知中心在原点的双曲线C的右焦点为F(4,0),离心率等于$\frac{4}{3}$,则C的方程是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{25}$=1 |
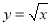 ,直线
,直线 及
及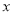 轴所围成图形的面积是( )
轴所围成图形的面积是( ) B.4 C.
B.4 C. D.6
D.6