题目内容
18.数列1,$\frac{1}{2}$,1,$\frac{1}{3}$,$\frac{2}{3}$,1,$\frac{1}{4}$,$\frac{1}{2}$,$\frac{3}{4}$,1,…,$\frac{1}{n}$,$\frac{2}{n}$,…1,…的第143项是$\frac{7}{17}$.分析 根据数列:1,$\frac{1}{2}$,1,$\frac{1}{3}$,$\frac{2}{3}$,1,$\frac{1}{4}$,$\frac{1}{2}$,$\frac{3}{4}$,1,…,$\frac{1}{n}$,$\frac{2}{n}$,…1,….可知:其分母为n的项共有n项,因此到分母为n+1的项的前面共有1+2+…+n项,即可得出答案.
解答 解:根据数列:1,$\frac{1}{2}$,1,$\frac{1}{3}$,$\frac{2}{3}$,1,$\frac{1}{4}$,$\frac{1}{2}$,$\frac{3}{4}$,1,…,$\frac{1}{n}$,$\frac{2}{n}$,…1,….
可知:其分母为n的项共有n项,因此到分母为n+1的项的前面共有1+2+…+n=$\frac{n(n+1)}{2}$项,
当n=16时,$\frac{16×(1+16)}{2}$=136,136+7=143,
故此数列的第143项是$\frac{7}{17}$.
故答案为:$\frac{7}{17}$.
点评 本题考查了通过观察分析猜想归纳求数列的通项公式、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
9.已知直角△ABC中,斜边AB=6,D为线段AB的中点,P为线段CD上任意一点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值为( )
| A. | -$\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | -2 | D. | 2 |
3.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | ($\frac{1}{3}$)-1=3 | C. | (-2)3=8 | D. | a6-a3=8 |
 已知某几何体的三视图如图所示(长度单位为:cm),则该几何体的体积为16cm3,表面积为34+6$\sqrt{5}$cm2.
已知某几何体的三视图如图所示(长度单位为:cm),则该几何体的体积为16cm3,表面积为34+6$\sqrt{5}$cm2.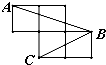 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为$\frac{\sqrt{2}}{2}$.
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为$\frac{\sqrt{2}}{2}$.