题目内容
10. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为$\frac{\sqrt{2}}{2}$.
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为$\frac{\sqrt{2}}{2}$.
分析 由已知可求AB,BC,从而可求sin∠ABD,cos∠CBD,cos∠ABD,sin∠CBD,由两角和的正弦函数公式即可得解.
解答 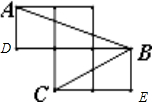 解:∵如图,可得:AB=$\sqrt{10}$,BC=$\sqrt{5}$
解:∵如图,可得:AB=$\sqrt{10}$,BC=$\sqrt{5}$
∴sin∠ABD=$\frac{1}{\sqrt{10}}$,cos∠CBD=$\frac{2}{\sqrt{5}}$,cos∠ABD=$\frac{3}{\sqrt{10}}$,sin∠CBD=$\frac{1}{\sqrt{5}}$,
∴sin∠ABC=sin(∠ABD+∠CBD)=sin∠ABDcos∠CBD+cos∠ABDsin∠CBD=$\frac{1}{\sqrt{10}}×\frac{2}{\sqrt{5}}+\frac{3}{\sqrt{10}}×\frac{1}{\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题主要考查了两角和的正弦函数公式的应用,属于基础题.

练习册系列答案
相关题目
1. 函数 f(x)=ax3+$\frac{1}{2}$x2的导函数为 f′(x),且 f(x) 在 x=-1 处取得极大值,设g(x)=$\frac{1}{f′(x)}$,执行如图所示的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
函数 f(x)=ax3+$\frac{1}{2}$x2的导函数为 f′(x),且 f(x) 在 x=-1 处取得极大值,设g(x)=$\frac{1}{f′(x)}$,执行如图所示的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
 函数 f(x)=ax3+$\frac{1}{2}$x2的导函数为 f′(x),且 f(x) 在 x=-1 处取得极大值,设g(x)=$\frac{1}{f′(x)}$,执行如图所示的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
函数 f(x)=ax3+$\frac{1}{2}$x2的导函数为 f′(x),且 f(x) 在 x=-1 处取得极大值,设g(x)=$\frac{1}{f′(x)}$,执行如图所示的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )| A. | n≤2014 | B. | n≤2015 | C. | n>2014 | D. | n>2015 |
2.已知x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x-y-1≤0\end{array}$,当目标函数z=$\sqrt{3}$ax+by({a>0,b>0})在该约束条件下取得最大值4时,a2+b2的最小值为( )
| A. | 8 | B. | 4 | C. | $\frac{{8\sqrt{3}}}{3}$ | D. | 2 |
7.在△ABC中,$\overrightarrow{AB}$=(k,1),$\overrightarrow{AC}$=(2,3),若∠A=90°,则k的值是( )
| A. | -5 | B. | 5 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |