题目内容
9．已知直角△ABC中，斜边AB=6，D为线段AB的中点，P为线段CD上任意一点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$的最小值为（ ）| A． | -$\frac{9}{2}$ | B． | $\frac{9}{2}$ | C． | -2 | D． | 2 |
分析 根据图形判断设|PC|=3-x，e则|PD|=x，$\overrightarrow{PD}$与$\overrightarrow{PC}$的夹角为π，0≤x≤3，运用数量积的运算得出函数式子（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$=-2x•（3-x），再利用基本不等式求解即可．
解答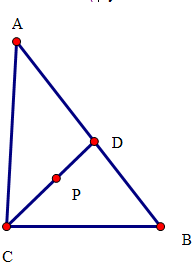 
解：∵直角△ABC中，斜边AB=6，D为线段AB的中点，
∴|CD|=3，$\overrightarrow{PA}$+$\overrightarrow{PB}$=2$\overrightarrow{PD}$，
∵P为线段CD上任意一点，
∴设|PC|=3-x，则|PD|=x，$\overrightarrow{PD}$与$\overrightarrow{PC}$的夹角为π，0≤x≤3，
∴（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$=-2x•（3-x），
∵x•（3-x）≤$\frac{9}{4}$，
∴-2x•（3-x）≥-2×$\frac{9}{4}$=-$\frac{9}{2}$．
故选：A．
点评 本题考查了平面向量的数量积，转化为函数求解，关键是根据图形得出向量的关系，属于容易题．
练习册系列答案
相关题目
17．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，3$\overrightarrow{a}$+$\frac{1}{5}$$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$垂直，则$\overrightarrow{a}$，$\overrightarrow{b}$夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2}{3}$π | D． | $\frac{5}{6}$π |
函数 f（x）=ax3+$\frac{1}{2}$x2的导函数为 f′（x），且 f（x） 在 x=-1 处取得极大值，设g（x）=$\frac{1}{f′（x）}$，执行如图所示的程序框图，若输出的结果大于$\frac{2014}{2015}$，则判断框内可填入的条件是（ ）