题目内容
12.已知实数x,y满足x2+y2=9(y≥0).试求m=$\frac{y+3}{x+1}$及b=2x+y的取值范围.分析 画出图形,利用表达式的几何意义,求解不等式的范围即可.
解答  解:实数x,y满足x2+y2=9(y≥0).满足的图形如图:
解:实数x,y满足x2+y2=9(y≥0).满足的图形如图:
m=$\frac{y+3}{x+1}$的几何意义是半圆上的点与(-1,-3)连线的斜率,
kPA=$\frac{0+3}{3+1}$=$\frac{3}{4}$,kPB=$\frac{0+3}{-3+1}$=$-\frac{3}{2}$
可得m∈[$\frac{3}{4},+∞$)∪(-∞,$-\frac{3}{2}$].
b=2x+y,与半圆相切或相交,
可得3=$\frac{|-b|}{\sqrt{5}}$,解得b=3$\sqrt{5}$,直线经过B时b取得最小值:-6.
所以m的范围是[$\frac{3}{4},+∞$)∪(-∞,$-\frac{3}{2}$].
b=2x+y的取值范围:[-6,3$\sqrt{5}$].
点评 本题考查直线与圆的位置关系的应用,简单详细规划的应用,考查计算能力.

练习册系列答案
相关题目
20.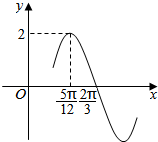 已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
 已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{π}{12}$] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{π}{12}$,$\frac{5π}{12}$] |
8.与不等式x2-4x-3≤0同解的不等式是( )
| A. | x-$\frac{3}{x}$≤4 | B. | |x-2|≤$\sqrt{7}$ | C. | x-4$\sqrt{x}$-3≤0 | D. | x4-4x2-3≤0 |