题目内容
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求实数![]() 、
、![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅲ)曲线![]() 上存在两点
上存在两点![]() 、
、![]() ,使得
,使得![]() 是以坐标原点
是以坐标原点![]() 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边![]() 的中点在
的中点在![]() 轴上,求实数
轴上,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时
时![]() 在[-1,2]上的最大值为2,
在[-1,2]上的最大值为2,
当![]() 时
时![]() 在[-1,2]上的最大值为
在[-1,2]上的最大值为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】试题分析:(1)利用导数几何意义: ![]() 可列等量关系.当
可列等量关系.当![]() 时,
时, ![]() 所以
所以![]() ,又
,又![]() 所以
所以![]() 因此
因此 ![]() (2)求分段函数最值,先分别讨论各区间函数最值,再比较大小,确定最值.当
(2)求分段函数最值,先分别讨论各区间函数最值,再比较大小,确定最值.当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,列表分析得
,列表分析得![]() 的最大值为
的最大值为![]() ,当
,当![]() 时,
时, ![]() ,需根据c的值确定函数最值,当
,需根据c的值确定函数最值,当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() ,当
,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() ,比较
,比较![]() 与2的大小得:当
与2的大小得:当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]() (3)利用坐标探求等量关系,确定坐标所在位置是解题关键.根据条件
(3)利用坐标探求等量关系,确定坐标所在位置是解题关键.根据条件![]() ,
, ![]() 的横坐标互为相反数,不妨设
的横坐标互为相反数,不妨设![]() ,
, ![]() ,
, ![]() .若
.若![]() ,则
,则![]() ,有
,有
![]() ,无解,若
,无解,若![]() ,则
,则![]() .有
.有![]() ,
, ![]() 取值范围是
取值范围是![]()
(1)当![]() 时,
时, ![]()
所以![]() ,又
,又![]()
所以![]() 因此
因此 ![]()
(2)当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,列表得:
,列表得:
x | -1 | (-1,0) | 0 |
|
|
| 1 |
| - | 0 | + | 0 | - | ||
| 2 | ↘ | ↗ |
| ↘ | 0 |
所以当![]() 时,
时, ![]() 的最大值为
的最大值为![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() ,
,
此时![]() 在
在![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .
.
令![]() ,则
,则![]() ,所以当
,所以当![]() 时,
时,
![]() 在
在![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
综上可知,当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
⑶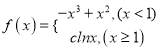 ,根据条件
,根据条件![]() ,
, ![]() 的横坐标互为相反数,不妨设
的横坐标互为相反数,不妨设![]() ,
, ![]() ,
, ![]() .
.
若![]() ,则
,则![]() ,
,
由![]() 是直角得,
是直角得, ![]() ,即
,即![]() ,
,
即![]() .此时无解;
.此时无解;
若![]() ,则
,则![]() .由于
.由于![]() 的中点在
的中点在![]() 轴上,且
轴上,且![]() ,所以
,所以![]() 点不可能在
点不可能在![]() 轴上,即
轴上,即![]() .同理有
.同理有![]() ,即
,即![]() ,
, ![]() .由于函数
.由于函数![]() 的值域是
的值域是![]() ,实数
,实数![]() 的取值范围是
的取值范围是![]() 即为所求.
即为所求.

【题目】国家“十三五”计划,提出创新兴国,实现中国创新,某市教育局为了提高学生的创新能力,把行动落到实处,举办一次物理、化学综合创新技能大赛,某校对其甲、乙、丙、丁四位学生的物理成绩(x)和化学成绩(y)进行回归分析,求得回归直线方程为y=1.5x﹣35.由于某种原因,成绩表(如表所示)中缺失了乙的物理和化学成绩.
甲 | 乙 | 丙 | 丁 | |
物理成绩(x) | 75 | m | 80 | 85 |
化学成绩(y) | 80 | n | 85 | 95 |
综合素质 | 155 | 160 | 165 | 180 |
(1)请设法还原乙的物理成绩m和化学成绩n;
(2)在全市物理化学科技创新比赛中,由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛,每场比赛均由赛事主办方从学校代表中随机抽两人参赛,每场比赛所抽的选手中,只要有一名选手的综合素质分高于160分,就能为所在学校赢得一枚荣誉奖章.若记比赛中赢得荣誉奖章的枚数为ξ,试根据上表所提供数据,预测该校所获奖章数ξ的分布列与数学期望.