题目内容
【题目】已知四棱锥P﹣ABCD及其三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P﹣ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D﹣AE﹣B的大小.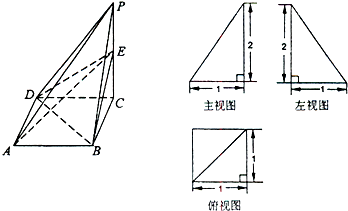
【答案】解:(I)由三视图知PC⊥面ABCD,
ABCD为正方形,且PC=2,AB=BC=1,
∴ ![]() .
.
(II)不论点E在何位置,都有BD⊥AE.
证明如下:
∵PC⊥面ABCD,BD面ABCD,∴PC⊥BD
而BD⊥AC,AC∩AE=A,∴BD⊥面ACE,
而AE面ACE,
∴BD⊥AE.
(III)连接AC,交BD于O.
由对称性,二面角D﹣AE﹣B是二面角O﹣AE﹣B的2倍,
设θ为二面角O﹣AE﹣B的平面角.
注意到B在面ACE上的射影为O,![]() ,
,![]() ,
,
∴ ![]() ,
,
∴θ=60°∴二面角D﹣AE﹣B是120°.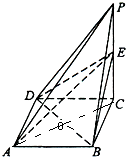
【解析】(I)由三视图知PC⊥面ABCD,ABCD为正方形,且PC=2,AB=BC=1,由此能求出四棱锥P﹣ABCD的体积.(II)不论点E在何位置,都有BD⊥AE.由已知得PC⊥BD,从而BD⊥面ACE,由此能证明BD⊥AE.(III)连接AC,交BD于O.由对称性,二面角D﹣AE﹣B是二面角O﹣AE﹣B的2倍,设θ为二面角O﹣AE﹣B的平面角.注意到B在面ACE上的射影为O,由 ![]() ,能求出二面角D﹣AE﹣B的大小.
,能求出二面角D﹣AE﹣B的大小.

练习册系列答案
相关题目