题目内容
【题目】已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.
(Ⅰ)求抛物线方程;
(Ⅱ)点P为准线上任意一点,AB为抛物线上过焦点的任意一条弦,设直线PA,PB,PF的斜率为k1,k2,k3,问是否存在实数λ,使得k1+k2=λk3恒成立.若存在,请求出λ的值;若不存在,请说明理由.
【答案】(1)抛物线方程为y2=4x;(2)见解析.
【解析】
![]() 由抛物线的定义,到焦点的距离等于到准线的距离即可求出
由抛物线的定义,到焦点的距离等于到准线的距离即可求出![]() ,即可得到方程
,即可得到方程
![]() 求出焦点和准线,设出直线
求出焦点和准线,设出直线![]() ,联立方程,消去
,联立方程,消去![]() 得到
得到![]() 的方程,运用韦达定理,设
的方程,运用韦达定理,设![]() ,
,![]() ,
,![]() ,运用斜率公式,化简整理,注意点在抛物线上,且全部转化为
,运用斜率公式,化简整理,注意点在抛物线上,且全部转化为![]() 的式子,即可判断
的式子,即可判断
(I)抛物线y2=2px(p>0)的焦点为(![]()
![]() ,0),准线为x=
,0),准线为x=![]()
![]() ,
,
由抛物线的定义可知:4=3![]() ,p=2
,p=2
∴抛物线方程为y2=4x;
(II)由于抛物线y2=4x的焦点F为(1,0),准线为x=﹣1,
设直线AB:x=my+1,与y2=4x联立,消去x,整理得:
y2﹣4my﹣4=0,
设A(x1,y1),B(x2,y2),P(﹣1,t),有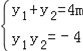
易知![]() ,而
,而![]()
=![]() =
=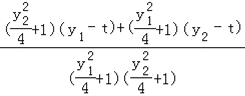
=![]() =2k3
=2k3
∴存在实数λ=2,使得k1+k2=λk3恒成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目