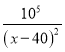题目内容

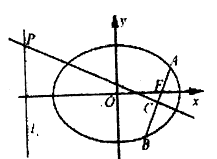
【题目】如图，在平面直角坐标系中，已知椭圆，直线，过右焦点的直线与椭圆交于两点，线段的垂直平分线分别交直线和于点．

（1）求弦长的最小值；

（2）在直线上任取一点，当的斜率时，求的值．

【答案】（1）；（2）．

【解析】

试题分析：（1）求椭圆的弦长，可分类，当斜率不存在时，得弦长为，当斜率存在时，设直线的方程为，将的方程代入椭圆方程，得的一元二次方程：，从而有（也可解出），弦长为，这样可以把弦长用表示出来，求出其最小值或证明它大于，说明是最小值；（2）由向量的数量积定义可得，由于，由（1）可得中点的坐标，从而得方程，又得点坐标，最后得长，得数量积．

试题解析：（1）①当轴时，；

②当与轴不垂直时，设直线的方程为，将的方程代入椭圆方程，得，

则的坐标为，

且．

综合①、②知，弦长的最小值为

（2）若，则的坐标为，

点的坐标为，

∴

∴

练习册系列答案
相关题目

【题目】已知函数．

⑴从区间内任取一个实数，设事件表示“函数在区间上有两个不同的零点”，求事件发生的概率；

⑵若联系掷两次一颗均匀的骰子（骰子六个面上标注的点数分别为）得到的点数分别为和，记事件表示“在上恒成立”，求事件发生的概率．

【题目】下列说法中，正确的有__________．（写出所有正确说法的序号）

①已知关于的不等式的角集为，则实数的取值范围是．

②已知等比数列的前项和为，则、、也构成等比数列．

③已知函数（其中且）在上单调递减，且关于的方程恰有两个不相等的实数解，则．

④已知，且，则的最小值为．

⑤在平面直角坐标系中， 为坐标原点， 则的取值范围是．

【题目】已知函数.

（1）当x∈[1，4]时，求函数的值域；

（2）如果对任意的x∈[1，4]，不等式恒成立，求实数k的取值范围

【题目】某班同学利用国庆节进行社会实践，对岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低硕族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：

组数

分组

低碳族的人数

占本组的频率

第一组

120

0.6

第二组

195

第三组

100

0.5

第四组

0.4

第五组

30

0.3

第六组

15

0.3

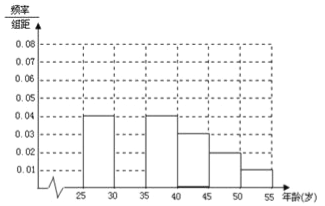
（1）补全频率分布直方图并求的值（直接写结果）；

（2）从年龄段在的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中至少有1人年龄在岁的概率．

【题目】某商品进货价每件50元，据市场调查，当销售价格（每件x元）在50≤ x ≤80时，每天售出的件数为P=，每天获得的利润为y（元）

（1）写出关于x的函数y的表达式；

（2）若想每天获得的利润最多，问售价应定为每件多少元？

【题目】在长方体中，分别是的中点，，过三点的的平面截去长方体的一个角后．得到如图所示的几何体，且这个几何体的体积为．

（1）求证：平面；

（2）求的长；

（3）在线段上是否存在点，使直线与垂直，如果存在，求线段的长，如果不存在，请说明理由．

【题目】如图所示，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC.E是PC的中点，作EF⊥PB交PB于点F.

（1)证明PA∥平面EDB；

（2)证明PB⊥平面EFD；

（3)求二面角C－PB－D的大小.

【题目】已知椭圆的中心在原点，焦点在轴上，离心率为，右焦点到右顶点的距离为．

（Ⅰ）求椭圆的标准方程；

（Ⅱ）是否存在与椭圆交于两点的直线：，使得成立？若存在，求出实数的取值范围，若不存在，请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网