题目内容
【题目】在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,过
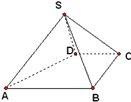
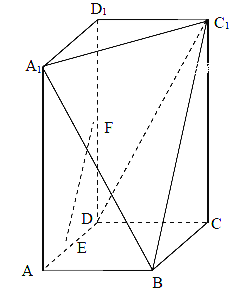
,过![]() 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体![]() ,且这个几何体的体积为
,且这个几何体的体积为![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的长;
的长;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与
与![]() 垂直,如果存在,求线段
垂直,如果存在,求线段![]() 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)证得![]() 是平行四边形,得出线线平行,利用线面平行的判定定理证明命题成立;(2)利用等体积转化
是平行四边形,得出线线平行,利用线面平行的判定定理证明命题成立;(2)利用等体积转化![]() ,求出
,求出![]() ;(3)在平面
;(3)在平面![]() 中作
中作![]() ,过
,过![]() 作
作![]() ,推出
,推出![]() ,证明
,证明![]() ,推出
,推出![]() 相似于
相似于![]() ,求得
,求得![]() .
.
试题解析:解:(1)在长方体![]() 中,可知
中,可知![]() ,由四边形
,由四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .因为
.因为![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() ,则
,则![]() ,
,
又![]() 面
面![]() 面
面![]() ,则
,则![]() 平面
平面![]() ............4分
............4分
(2)∵ ,
,
∴![]() ..................8分
..................8分
(3)在平面![]() 中作
中作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,∴
,∴![]() ,而
,而
![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
∵四边形![]() 为直角梯形,且高
为直角梯形,且高![]() ,∴
,∴![]() .......... 12分
.......... 12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目