Question

【题目】分别求出适合下列条件的直线方程： （Ⅰ）经过点P（﹣3，2）且在x轴上的截距等于在y轴上截距的2倍；
（Ⅱ）经过直线2x+7y﹣4=0与7x﹣21y﹣1=0的交点，且和A（﹣3，1），B（5，7）等距离．

Answer 1

【答案】解：（Ⅰ）当直线不过原点时，设所求直线方程为 + =1，

将（﹣3，2）代入所设方程，解得a= ，此时，直线方程为x+2y﹣1=0．

当直线过原点时，斜率k=﹣ ，直线方程为y=﹣ x，即2x+3y=0，

综上可知，所求直线方程为x+2y﹣1=0或2x+3y=0．

（Ⅱ）有 解得交点坐标为（1， ），

当直线l的斜率k存在时，设l的方程是y﹣ =k（x﹣1），即7kx﹣7y+（2﹣7k）=0，

由A、B两点到直线l的距离相等得 ，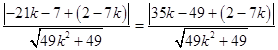

解得k= ，当斜率k不存在时，即直线平行于y轴，方程为x=1时也满足条件．

所以直线l的方程是21x﹣28y﹣13=0或x=1

【解析】（Ⅰ）分别讨论直线过原点和不过原点两种情况，设出直线方程，解出即可；（Ⅱ）先求出直线的交点坐标，设出直线方程，再根据点到直线的距离公式求出斜率k即可．
【考点精析】利用一般式方程对题目进行判断即可得到答案，需要熟知直线的一般式方程：关于的二元一次方程（A，B不同时为0）．