Question

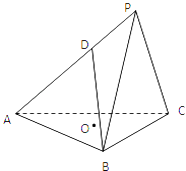
【题目】四边形ABCD是正方形，△PAB与△PAD均是以A为直角顶点的等腰直角三角形，点F是PB的中点，点E是边BC上的任意一点．

（1）求证：AF⊥EF；
（2）求二面角A﹣PC﹣B的平面角．

Answer 1

【答案】
（1）证明：∵四边形ABCD是正方形，△PAB与△PAD均是以A为直角顶点的等腰直角三角形，

∴PA⊥AD，PA⊥AB，又AD∩AB=A，AB⊥BC，

∴PA⊥平面ABCD，又BC面ABCD，∴PA⊥BC，

∵AB∩PA=A，∴BC⊥面PAB，

∴BC⊥AF，

∵△PAB是以A为直角顶点的等腰直角三角形，F是PB中点，

∴AF⊥PB，

又PB∩BC=B，∴AF⊥平面PBC，

∵EF平面PBC，∴AF⊥EF

（2）解：以A为原点，AD为x轴，AB为y轴，P为z轴，

建立空间直角坐标系，

设AB=1，则A（0，0，0），B（0，1，0），C（1，1，0），P（0，0，1），

=（0，0，1）， =（1，1，0），

设平面APC的法向量 =（x，y，z），

则 ，取x=1，得 =（1，﹣1，0），

=（0，1，﹣1）， =（1，1，﹣1），

设平面PBC的法向量 =（a，b，c），

则 ，取b=1，得 =（0，1，1），

|cos＜ ＞|=| |= ，

∴＜ ＞=60°，

∴二面角A﹣PC﹣B的平面角为60°．

【解析】（1）由已知得PA⊥AD，PA⊥AB，AB⊥BC，从而PA⊥BC，进而BC⊥面PAB，又AF⊥PB，由此能证明AF⊥EF．（2）以A为原点，AD为x轴，AB为y轴，P为z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣PC﹣B的平面角．