题目内容
【题目】如图,等边三角形OAB的边长为8 ![]() ,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.
,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点. 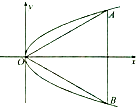
(1)证明:A、B两点关于x轴对称;
(2)求抛物线E的方程.
【答案】
(1)证明:设A(x1,y1)、B(x2,y2),
∵|OA|=|OB|,∴x12+y12=x22+y22.
又∵y12=2px1,y22=2px2,
∴x22﹣x12+2p(x2﹣x1)=0,
即(x2﹣x1)(x1+x2+2p)=0.
又∵x1、x2与p同号,∴x1+x2+2p≠0.
∴x2﹣x1=0,即x1=x2.
由抛物线对称性,知点A、B关于x轴对称.
(2)解:由(1)知∠AOx=30°,则y2=2px,x=6p,
∴y= ![]() x,y=2
x,y=2 ![]() p.
p.
∴A(6p,2 ![]() p),
p),
∵等边三角形OAB的边长为8 ![]() ,
,
∴(6p)2+(2 ![]() p)=(8
p)=(8 ![]() )2.
)2.
∴p=2,
∴抛物线E的方程为y2=4x
【解析】(1)A(x1 , y1)、B(x2 , y2)根据|OA|=|OB|可得x12+y12=x22+y22 . 由于A,B都在抛物线上进而满足y12=2px1 , y22=2px2 , 整理可得(x2﹣x1)(x1+x2+2p)=0.根据x1、x2与p同号可知x1+x2+2p≠0进而可得x1=x2 . 根据抛物线对称性,知点A、B关于x轴对称.(2)由(1)可知∠AOx=30°,进而根据抛物线和直线方程求得点A的坐标,利用等边三角形OAB的边长为8 ![]() ,可得p,即可求抛物线E的方程.
,可得p,即可求抛物线E的方程.

练习册系列答案
相关题目


