题目内容
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ![]() ,底面是边长为
,底面是边长为 ![]() 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:如图所示,
∵AA1⊥底面A1B1C1 , ∴∠APA1为PA与平面A1B1C1所成角,
∵平面ABC∥平面A1B1C1 , ∴∠APA1为PA与平面ABC所成角.
∵ ![]() =
= ![]() =
= ![]() .
.
∴V三棱柱ABC﹣A1B1C1= ![]() =
= ![]() ,解得
,解得 ![]() .
.
又P为底面正三角形A1B1C1的中心,∴ ![]() =
= ![]() =1,
=1,
在Rt△AA1P中, ![]() ,
,
∴ ![]() .
.
故选B.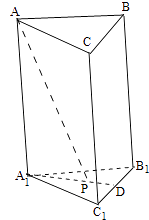
利用三棱柱ABC﹣A1B1C1的侧棱与底面垂直和线面角的定义可知,∠APA1为PA与平面A1B1C1所成角,即为∠APA1为PA与平面ABC所成角.利用三棱锥的体积计算公式可得AA1 , 再利用正三角形的性质可得A1P,在Rt△AA1P中,利用tan∠APA1= ![]() 即可得出.
即可得出.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目