题目内容
17.已知x,y满足不等式组$\left\{\begin{array}{l}{5x+3y≤15}\\{y≤x+1}\\{x-5y≤3}\end{array}\right.$,求z=3x+5y的最大值和最小值.分析 作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到最大值和最小值.
解答 解:不等式组对应的平面区域如图: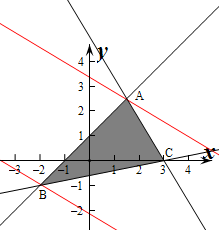
由z=3x+5y得y=$-\frac{3}{5}$$x+\frac{z}{5}$,
平移直线y=$-\frac{3}{5}$$x+\frac{z}{5}$,则由图象可知当直线y=$-\frac{3}{5}$$x+\frac{z}{5}$经过点A时直线y=$-\frac{3}{5}$$x+\frac{z}{5}$的截距最大,
此时z最大,当经过点B时,直线的截距最小,此时z最小.
由$\left\{\begin{array}{l}{y=x+1}\\{5x+3y=15}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{5}{2}}\end{array}\right.$,即A($\frac{3}{2}$,$\frac{5}{2}$),
此时最大值z=3×$\frac{3}{2}$+5×$\frac{5}{2}$=17,
由$\left\{\begin{array}{l}{y=x+1}\\{x-5y=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,即B(-2,-1),
此时最小值z=3×(-2)+5×(-1)=-11.
点评 本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
5.若直线$\left\{\begin{array}{l}x=1-2t\\ y=2+3t\end{array}\right.$(t为参数)与直线4x+ky=1垂直,则常数k=( )
| A. | -6 | B. | $-\frac{1}{6}$ | C. | 6 | D. | $\frac{1}{6}$ |
9.一个盒子中有20个大小形状相同的小球,其中5个红球,5个黄球,10个蓝球,从盒子中任取一球,若它不是红球,则它是蓝球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
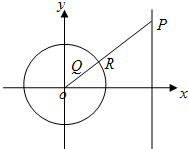 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.