题目内容
【题目】若函数f（x）= 
是奇函数，则使f（x）＞3成立的x的取值范围为（ ）
A.（﹣∞，﹣1）
B.（﹣1，0）
C.（0，1）
D.（1，+∞）
【答案】C
【解析】解：∵f（x）= 
是奇函数，
∴f（﹣x）=﹣f（x）
即 
整理可得， 
∴1﹣a2x=a﹣2x
∴a=1，
∴f（x）= 
∵f（x））= ＞3
∴ ﹣3= 
＞0，
整理可得， 
，
∴1＜2x＜2
解可得，0＜x＜1
故选：C
【考点精析】通过灵活运用函数单调性的性质和函数奇偶性的性质，掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇即可以解答此题．
阅读快车系列答案
【题目】【2017湖南长沙二模】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等极如下表：
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：
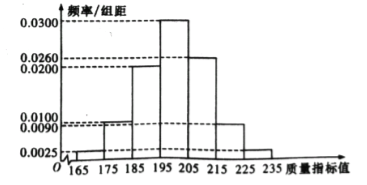
（1）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定？
（2）在样本中，按产品等极用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（3）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值
近似满足
，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
【题目】【2017北京西城区5月模拟】某大学为调研学生在
，
两家餐厅用餐的满意度，从在
，
两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分.
整理评分数据，将分数以10为组距分成6组：
，
，
，
，
，
，得到
餐厅分数的频率分布直方图，和
餐厅分数的频数分布表：
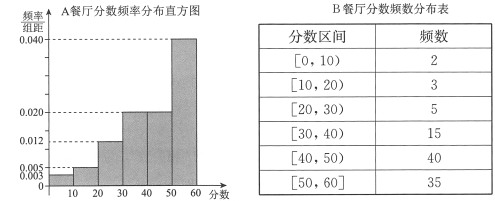
定义学生对餐厅评价的“满意度指数”如下：
分数 |
|
|
|
满意度指数 |
|
|
|
（Ⅰ）在抽样的100人中，求对
餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在
，
两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对
餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从
，
两家餐厅中选择一家用餐，你会选择哪一家？说明理由.
