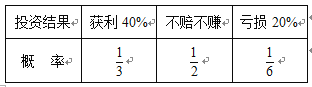
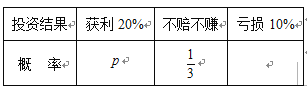
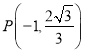题目内容
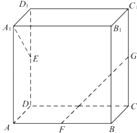
【题目】在长方体ABCD﹣A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值. 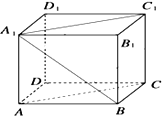
【答案】解:连接BD,BD∩AC=O,连接A1O, 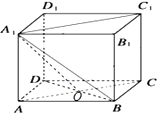
则BD⊥AC,BD⊥平面ACC1A1 , ∠BA1O是直线A1B与平面ACC1A1所成角.
∵DA=DC=4,DD1=3,
∴BO=2 ![]() ,A1B=
,A1B= ![]() ,
,
∴直线A1B与平面ACC1A1所成角的正弦值= ![]() .
.
【解析】连接BD,BD∩AC=O,连接A1O,则BD⊥AC,BD⊥平面ACC1A1 , ∠BA1O是直线A1B与平面ACC1A1所成角.
【考点精析】掌握空间角的异面直线所成的角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则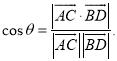 .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目