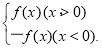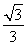题目内容
已知函数f(x)＝
.
(1)若f(x)>k的解集为{x|x<－3，或x>－2}，求k的值；
(2)对任意x>0，f(x)≤t恒成立，求t的取值范围．
（1）k＝－
（2）
【解析】(1)f(x)>k?kx2－2x＋6k<0.
由已知{x|x<－3，或x>－2}是其解集，得kx2－2x＋6k＝0的两根是－3，－2，由根与系数的关系可知(－2)＋(－3)＝
，即k＝－.
(2)∵x>0，f(x)＝
＝
≤
＝
.当且仅当x＝
时取等号，
由已知f(x)≤t对任意x>0恒成立，故t≥
.
即t的取值范围是.
练习册系列答案
手拉手全优练考卷系列答案
相关题目
