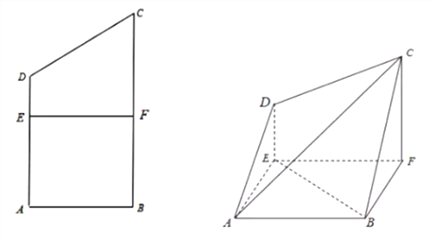
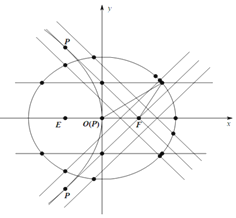
题目内容
【题目】【2014福建,文22】已知函数![]() (
(![]() 为常数)的图像与
为常数)的图像与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]()
(3)证明:对任意给定的正数![]() ,总存在
,总存在![]() ,使得当
,使得当![]() 时,恒有
时,恒有![]()
【答案】(1)当![]() 时,
时,![]() 有极小值
有极小值![]() ,
,![]() 无极大值.
无极大值.
(2)见解析.(3)见解析.
【解析】
试题分析:(1)由![]() ,得
,得![]() .
.
从而![]() .
.
令![]() ,得驻点
,得驻点![]() .讨论可知:
.讨论可知:
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
当![]() 时,
时,![]() 有极小值
有极小值![]() ,
,![]() 无极大值.
无极大值.
(2)令![]() ,则
,则![]() .
.
根据![]() ,知
,知![]() 在R上单调递增,又
在R上单调递增,又![]() ,
,
当![]() 时,由
时,由![]() ,即得.
,即得.
(3)思路一:对任意给定的正数c,取![]() ,
,
根据![]() .得到当
.得到当![]() 时,
时,![]() .
.
思路二:令![]() ,转化得到只需
,转化得到只需![]() 成立.
成立.
分![]() ,
,![]() ,应用导数研究
,应用导数研究![]() 的单调性.
的单调性.
思路三:就①![]() ,②
,②![]() ,加以讨论.
,加以讨论.
试题解析:
【解法一】
(1)由![]() ,得
,得![]() .
.
又![]() ,得
,得![]() .
.
所以![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以当![]() 时,
时,![]() 有极小值,
有极小值,
且极小值为![]() ,
,
![]() 无极大值.
无极大值.
(2)令![]() ,则
,则![]() .
.
由(1)得,![]() ,即
,即![]() .
.
所以![]() 在R上单调递增,又
在R上单调递增,又![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() .
.
(3)对任意给定的正数c,取![]() ,
,
由(2)知,当![]() 时,
时,![]() .
.
所以当![]() 时,
时,![]() ,即
,即![]() .
.
因此,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
【解法二】
(1)同解法一.
(2)同解法一.
(3)令![]() ,要使不等式
,要使不等式![]() 成立,只要
成立,只要![]() 成立.
成立.
而要使![]() 成立,则只需
成立,则只需![]() ,即
,即![]() 成立.
成立.
①若![]() ,则
,则![]() ,易知当
,易知当![]() 时,
时,![]() 成立.
成立.
即对任意![]() ,取
,取![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
②若![]() ,令
,令![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调递增.
内单调递增.
取![]() ,
,
![]() ,
,
易知![]() ,
,![]() ,所以
,所以![]() .
.
因此对任意![]() ,取
,取![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
综上,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
【解法三】
(1)同解法一.
(2)同解法一.
(3)①若![]() ,取
,取![]() ,
,
由(2)的证明过程知,![]() ,
,
所以当![]() 时,有
时,有![]() ,即
,即![]() .
.
②若![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() 得
得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
取![]() ,
,
![]() ,
,
易知![]() ,又
,又![]() 在
在![]() 内单调递增,
内单调递增,
所以当![]() 时,恒有
时,恒有![]() ,即
,即![]() .
.
综上,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
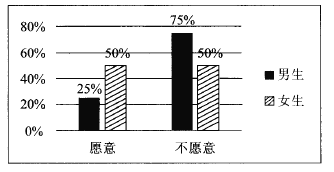
(1)根据条件完成下列![]()
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为![]()
,记甲通过的关数为![]()
,求![]()
的分布列和数学期望.
参考公式与数据:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
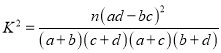
.