题目内容
【题目】(本小题满分14分)
设椭圆![]() 的离心率为
的离心率为![]() ,其左焦点
,其左焦点![]() 与抛物线
与抛物线![]() 的焦点相同.
的焦点相同.
(1)求此椭圆的方程;
(2)若过此椭圆的右焦点![]() 的直线
的直线![]() 与曲线
与曲线![]() 只有一个交点
只有一个交点![]() ,则
,则
①求直线![]() 的方程;
的方程;
②椭圆上是否存在点![]() ,使得
,使得![]() ,若存在,请说明一共有几个点;若不存在,请说明理由.
,若存在,请说明一共有几个点;若不存在,请说明理由.
【答案】(1)![]()
(2)①![]() 或
或![]() 或
或![]() .
.
②12个
【解析】
试题分析:对于第一问中的椭圆方程,根据抛物线的焦点坐标求出![]() 的值,根据离心率的值,得出
的值,根据离心率的值,得出![]() 的值,从而得出
的值,从而得出![]() 的值,得到相应的椭圆方程,对于第二问,根据题的条件,设出直线的方程,当直线和抛物线相切时,一种情况,联立式子,对应的二次方程有两个相等实根,判别式等于0,一种是直线和抛物线的对称轴平行即可得结果;根据所求的直线方程,可以得出对应的交点P的坐标,因为F点是已知的,所以三角形的底边FP的长度已经确定,要想面积是所给的值,可以得出点M到此直线的距离,建立相应的等量关系,从而得出点的个数.
的值,得到相应的椭圆方程,对于第二问,根据题的条件,设出直线的方程,当直线和抛物线相切时,一种情况,联立式子,对应的二次方程有两个相等实根,判别式等于0,一种是直线和抛物线的对称轴平行即可得结果;根据所求的直线方程,可以得出对应的交点P的坐标,因为F点是已知的,所以三角形的底边FP的长度已经确定,要想面积是所给的值,可以得出点M到此直线的距离,建立相应的等量关系,从而得出点的个数.
试题解析:
解:(1)抛物线![]() 的焦点为
的焦点为![]() ,
,
所以![]() . (1分)
. (1分)
由![]() ,得
,得![]() , (2分)
, (2分)
所以![]() (3分)
(3分)
因此,所求椭圆的方程为![]() (*)(4分)
(*)(4分)
(2)①椭圆的右焦点为![]() ,过点
,过点![]() 与
与![]() 轴平行的直线显然与曲线
轴平行的直线显然与曲线![]() 没有交点.设直线
没有交点.设直线![]() 的斜率为
的斜率为![]() . (5分)
. (5分)
当![]() 时,则直线
时,则直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 只有一个交点
只有一个交点![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() ; (6分)
; (6分)
当![]() 时,因直线
时,因直线![]() 过点
过点![]() ,故可设其方程为
,故可设其方程为![]() ,将其代入
,将其代入![]() 消去
消去![]() ,得
,得![]() .
.
因为直线![]() 与曲线
与曲线![]() 只有一个交点
只有一个交点![]() ,所以判别式
,所以判别式![]() ,于是
,于是![]() ,即直线
,即直线![]() 的方程为
的方程为![]() 或
或![]() . (7分)
. (7分)
因此,所求的直线![]() 的方程为
的方程为![]() 或
或![]() 或
或![]() . (8分)
. (8分)
②由①可求出点![]() 的坐标是
的坐标是![]() 或
或![]() 或
或![]() .
.
当点![]() 的坐标为
的坐标为![]() 时,则
时,则![]() .于是
.于是![]() =
=![]() ,从而
,从而![]() ,代入(*)式联立:
,代入(*)式联立: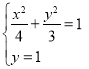 或
或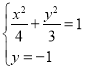 ,求得
,求得![]() ,此时满足条件的点
,此时满足条件的点![]() 有4个:
有4个:
 . (10分)
. (10分)
当点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,点
,点![]() 到直线
到直线![]() :
:![]() 的距离是
的距离是![]() ,于是有
,于是有![]() ,
,
从而![]() ,与(*)式联立:
,与(*)式联立: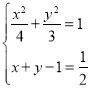 或
或 解之,可求出满足条件的点
解之,可求出满足条件的点![]() 有4个:
有4个:
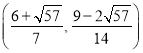 ,
,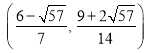 ,
,![]() ,
,![]() . (12分)
. (12分)
当点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,点
,点![]() 到直线
到直线![]() :
:![]() 的距离是
的距离是![]() ,于是有
,于是有![]() ,
,
从而![]() ,与(*)式联立:
,与(*)式联立: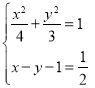 或
或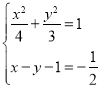 ,
,
解之,可求出满足条件的点![]() 有4个:
有4个:
 ,
,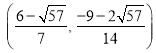 ,
,![]() ,
,![]() . (14分)
. (14分)
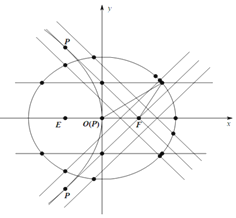
综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点![]() 共有12个.图上椭圆上的12个点即为所求.
共有12个.图上椭圆上的12个点即为所求.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案