题目内容
【题目】如图,矩形![]() 中,
中,![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置.
的位置.
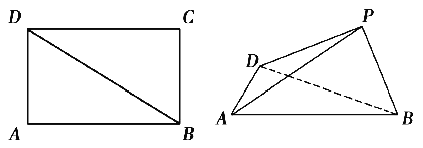
(1)若![]() ,求三棱锥
,求三棱锥![]() 体积的最大值;
体积的最大值;
(2)若![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
【答案】(1) ![]() ; (2)证明见解析
; (2)证明见解析
【解析】
(1)过P作PO⊥BD于O,求出PO![]() ,当PO⊥平面ABD时,三棱锥P﹣ABD体积最大,由此能求出三棱锥P﹣ABD体积的最大值.
,当PO⊥平面ABD时,三棱锥P﹣ABD体积最大,由此能求出三棱锥P﹣ABD体积的最大值.
(2)推导出PD⊥PB,PA⊥PB,从而PB⊥平面PAD,推导出AD⊥平面PAB,由此能证明平面PAB⊥平面ABD.
(1)过P作PO⊥BD于O,则POBD=PBPD,
解得PO![]() ,
,
当PO⊥平面ABD时,三棱锥P﹣ABD体积最大,
∴三棱锥P﹣ABD体积的最大值为:
VP﹣ABD![]() .
.
(2)在△PBD中,PD⊥PB,
又PA⊥PB,PA∩PB=P,
PA,PD平面PAD,
∴PB⊥平面PAD,
∵PB⊥AD,又AB⊥AD,AB∩PB=B,
∴AD⊥平面PAB,
又AD平面ABD,∴平面PAB⊥平面ABD.


练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目