题目内容
【题目】设函数![]() ,其中
,其中![]() 表示
表示![]() 中的最小者.下列说法错误的是
中的最小者.下列说法错误的是
A. 函数![]() 为偶函数 B. 若
为偶函数 B. 若![]() 时,有
时,有![]()
C. 若![]() 时,
时,![]() D. 若
D. 若![]() 时,
时,![]()
【答案】D
【解析】分析:由题意结合新定义的知识首先画出函数f(x)的图像,然后结合图像逐一分析所给的选项即可求得最终结果.
详解:结合新定义的运算绘制函数f(x)的图像如图1中实线部分所示,
观察函数图像可知函数图像关于y轴对称,则函数为偶函数,选项A的说法正确;
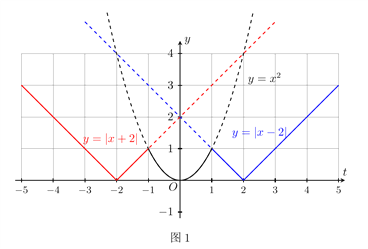
对于选项B,
若![]() ,则
,则![]() ,此时
,此时![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() ,
,
如图2所示,观察可得,恒有![]() ,选项B的说法正确;
,选项B的说法正确;
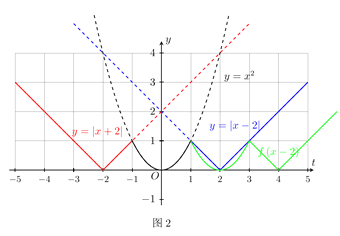
对于选项C,由于函数为偶函数,故只需考查![]() 时不等式是否成立即可,
时不等式是否成立即可,
若![]() ,则
,则![]() ,此时
,此时![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() ,
,
如图3所示,观察可得,恒有![]() ,选项C的说法正确;
,选项C的说法正确;

对于选项D,
若![]() ,则
,则![]() ,
,![]() ,
,
不满足![]() ,选项D的说法错误.
,选项D的说法错误.
本题选择D选项.

练习册系列答案
相关题目
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值都不超过
的差,若差值的绝对值都不超过![]() ,则称所求方程是“恰当回归方程”.
,则称所求方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间不相邻的概率;
组数据的间隔时间不相邻的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)为了使等候的乘客不超过![]() 人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟.
人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟.
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,![]() .
.