题目内容
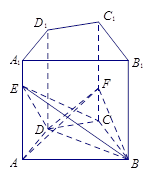
在如图的多面体中, 平面
平面 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 是
是 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
 平面
平面 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求证:
 ;
;(3)求三棱锥
 的体积.
的体积.(1)详见解析;(2)详见解析;(3)三棱锥 的体积为
的体积为 .
.
 的体积为
的体积为 .
.试题分析:(1)证明四边形
 为平行四边形,进而得到
为平行四边形,进而得到 ,再利用直线与平面平行的判定定理得到
,再利用直线与平面平行的判定定理得到 平面
平面 ;(2)过点
;(2)过点 作
作 交
交 于点
于点 ,连接
,连接 、
、 、
、 ,先证明
,先证明 平面
平面 ,于是得到
,于是得到 平面
平面 ,从而得到
,从而得到 ,再证明四边形
,再证明四边形 为菱形,从而得到
为菱形,从而得到 ,利用直线与平面垂直的判定定理得到
,利用直线与平面垂直的判定定理得到 平面
平面 ,从而得到
,从而得到 ;(3)由
;(3)由 平面
平面 ,由
,由 ,得到
,得到 平面
平面 ,从而将三棱锥
,从而将三棱锥 的体积的计算变换成以点
的体积的计算变换成以点 为顶点,以
为顶点,以 所在平面为底面的三棱锥来计算体积.
所在平面为底面的三棱锥来计算体积.试题解析:(1)∵AD∥EF,EF∥BC,∴AD∥BC.
又∵BC=2AD,G是BC的中点,∴AD//BG,
∴四边形ADGB是平行四边形,∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,∴AB∥平面DEG.

(2)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,∴AE⊥平面BCFE.
过D作DH∥AE交EF于H,则DH⊥平面BCFE.
∵EG?平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG,
又BH∩DH=H,BH?平面BHD,DH?平面BHD,∴EG⊥平面BHD.
∵BD?平面BHD,∴BD⊥EG.(10分)
(3)∵
 ⊥平面
⊥平面 ,EF//AD,∴AD⊥平面
,EF//AD,∴AD⊥平面 ,故三棱锥A-BED的高为AD
,故三棱锥A-BED的高为AD∵
 ,∴S△AEB =
,∴S△AEB = =
=
∴
 =
= S△AEB=
S△AEB= (14分)
(14分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
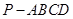 的底面是正方形,
的底面是正方形,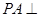 底面
底面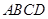 ,
,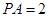 ,
,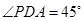 ,点
,点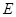 、
、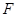 分别为棱
分别为棱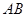 、
、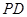 的中点.
的中点.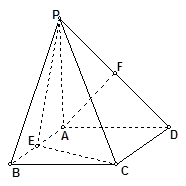
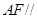 平面
平面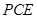 ;
;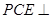 平面
平面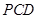 ;
;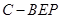 的体积.
的体积.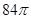 ,则圆台较小底面的面积为 .
,则圆台较小底面的面积为 .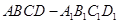 中,点
中,点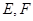 分别在
分别在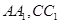 上,且
上,且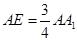 ,
,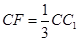 ,点
,点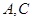 到
到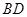 的距离之比为3:2,则三棱锥
的距离之比为3:2,则三棱锥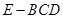 和
和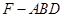 的体积比
的体积比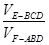 =" __" ___.
=" __" ___.
 种侧棱垂直于底面,
种侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱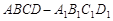 的面对角线
的面对角线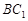 上运动,则下列四个命题:
上运动,则下列四个命题: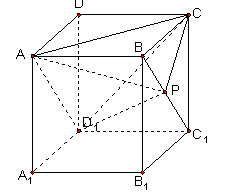
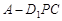 的体积不变;
的体积不变;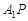 ∥平面
∥平面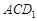 ;
;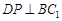 ;
;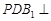 平面
平面 的面对角线
的面对角线 上存在一点P使得
上存在一点P使得 最短,则
最短,则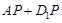 的最小值 .
的最小值 . 绕直线
绕直线 旋转一周所得的几何体的体积为( )
旋转一周所得的几何体的体积为( )



