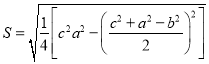题目内容
【题目】某小组共7人,利用假期参加义工活动,已知参加义工活动的次数为1,2,3的人数分别为2,2,3.现从这7人中随机选出2人作为该组代表参加座谈会:
(Ⅰ)设A为事件“选出的2人参加义工活动的次数之和为4”,求事件A发生的概率;
(Ⅱ)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列及数学期望.
【答案】(Ⅰ)![]() ; (Ⅱ)见解析
; (Ⅱ)见解析
【解析】
( I)由互斥事件的概率计算公式求出事件A发生的概率;(Ⅱ)根据题意知随机变量X的所有可能取值,计算对应的概率值,写出分布列,计算数学期望值.
(I)由已知得:P![]() ,
,
∴事件A发生的概率为![]() ;
;
(Ⅱ)随机变量X的所有可能取值为0,1,2;
计算![]() ,
,
P(X=1)![]() ,
,
P(X=2)![]() ;
;
∴随机变量X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
∴随机变量X的数学期望为
E(X)=0![]() 1
1![]() 2
2![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目