题目内容
【题目】已知公比为正数的等比数列
，首项
，前n项和为
，且
，
，
成等差数列.
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，求数列
的前n项和
【答案】（Ⅰ）an＝6×（
）n，（Ⅱ）Tn＝2﹣（n+2）（）n
【解析】
（Ⅰ）设公比为q＞0，由等比数列的通项公式和等差数列中项的性质，解方程可得q，即可得到所求通项公式；（Ⅱ）求得bn
n（）n，运用数列的求和方法：错位相减法，结合等比数列的求和公式，化简整理即可得到所求和．
（Ⅰ）an＝6×（）n，（Ⅱ）Tn＝2﹣（n+2）（）n
依题意公比为正数的等比数列{an}（n∈N*），首项
＝3，
设an＝3qn﹣1，
∵
，
，
成等差数列，
∴2（）＝+
即2（
）＝(
+（
），
化简得4
＝
，
从而4q2＝1，解得q＝±，
∵{an}（n∈N*）公比为正数，
∴q
，an＝6×（）n，n∈N*；
（Ⅱ）bnn（
）n，
则Tn＝1（）+2（）2+3（）3+…+（n﹣1）（）n﹣1+n（）n，
Tn＝1（）2+2（）3+3（）4+…+（n﹣1）（）n+n（）n+1，
两式相减可得Tn
（）2+（）3+（）4+…+（）n﹣n（）n+1
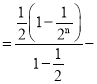n（）n+1，
化简可得Tn＝2﹣（n+2）（）n．
练习册系列答案
相关题目
