题目内容
【题目】已知函数![]() (a,b为常数),
(a,b为常数),
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)在(1)的条件下,![]() 有两个不相等的实根,求b的取值范围;
有两个不相等的实根,求b的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
【答案】(1)增区间为![]() 和
和![]() ,减区间为
,减区间为![]() 和
和![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)当a=1时,代入F(x)并求导,令![]() 和
和![]() 可得函数
可得函数![]() 的单调区间;
的单调区间;
(2)当a=1时,代入F(x)=0有两个不相等的实根,分离参数可得![]() ,记
,记![]() ,转化为直线
,转化为直线![]() 与
与![]() 的图象有且只有两个公共点,对函数
的图象有且只有两个公共点,对函数![]() 求导,研究其单调性,得出其图象变化规律及函数的极值,判断出图象与
求导,研究其单调性,得出其图象变化规律及函数的极值,判断出图象与![]() 有两个交点的情况数形结合即可求出范围.
有两个交点的情况数形结合即可求出范围.
(3)对任意的a∈[-1,0],不等式F(x)≥-8在[-2,2]上恒成立,故依据单调性判断出函数的最小值,令最小值大于等于-8即可解出参数b的取值范围.
(1)当![]() 时,
时,![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
![]() 的增区间为
的增区间为![]() 和
和![]() ,减区间为
,减区间为![]() 和
和![]() .
.
(2)由(1)a=1时,代入![]() ,
,
分离参数可得![]() ;
;
记![]() ,则
,则![]() ,
,
当x变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
x |
|
|
| 0 |
| 4 |
|
|
| 0 |
| 0 |
| 0 |
|
|
| 极小值 |
| 极大值0 |
| 极小值 |
|
由已知,知直线![]() 与
与![]() 的图象有且只有两个公共点,
的图象有且只有两个公共点,
所以,![]() ,或
,或![]() ,
,
![]() 的取值范围为
的取值范围为![]() .
.
(3)因为![]() ,
,
令![]() ,
,
则有![]() ,
,
当![]() 时,可知
时,可知![]() ,
,
![]() 恒成立,
恒成立,
![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 在
在![]() 内递增,在
内递增,在![]() 内递减,
内递减,
∵![]() ,
,
![]() ,
,
∴![]()
![]() 在
在![]() 上的最小值
上的最小值![]() 恒成立,
恒成立,
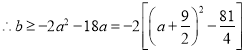 ,
,
当![]() 时,
时,![]() 取最大值16,
取最大值16,
所以b的取值范围为![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费(元) |
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 140 | 40 | 12 | 6 | 2 |
该保险公司这种保险的赔付规定如下表:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
| 0 |
将所抽样本的频率视为概率。
(1)求本年度—续保人保费的平均值的估计值;
(2)求本年度—续保人所获赔付金额的平均值的估计值;
(3)据统计今年有100万投保人进行续保,若该公司此险种的纯收益不少于900万元,求![]() 的最小值(纯收益=总入保额-总赔付额)。
的最小值(纯收益=总入保额-总赔付额)。