题目内容

5．若x+y+z=0，则x3+y3+z3=（　　）
A．0B．x2y+y2z+z2xC．x2+y2+z2D．3xyz

分析 利用x3+y3+z3=（x+y）[（x+y）2-3xy]+z3=（x+y）3-3xy（x+y）+z3，即可得出结论．

解答 解：∵x+y+z=0，
∴x3+y3+z3=（x+y）[（x+y）2-3xy]+z3=（x+y）3-3xy（x+y）+z3，
∴x3+y3+z3=3xyz．
故选：D．

点评 本题考查代数式的化简，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
15．某一几何体的三视图如图所示，按照给出的尺寸（单位：cm），则这个几何体的体积为（　　）
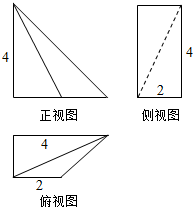
A．8cm3B．$\frac{40}{3}$cm3C．12cm3D．$\frac{50}{3}$cm3
16．求下列函数的最值与值域：
（1）y=4-$\sqrt{3+2x-{x}^{2}}$；
（2）y=2x-$\sqrt{1-2x}$；
（3）y=x+$\frac{4}{x}$；
（4）y=$\frac{{3}^{x}}{{3}^{x}+1}$．
13．已知命题p：关于x的方程a2x2-ax-2=0在x∈[-1，1]上有解；命题q：只有一个实数x满足不等式x2+2ax+2a≤0．
（1）若“p且q”是真命题，求实数a的取值范围；
（2）若“p或q”是假命题，求实数a的取值范围．
20．下列命题中正确的是（　　）
A．若a，b，c成等差数列，则a2，b2，c2成等差数列
B．若a，b，c成等差数列，则log2a，log2b，log2c成等差数列
C．若a，b，c成等差数列，则a+2，b+2，c+2成等差数列
D．若a，b，c成等差数列，则2a，2b，2c成等差数列
10．满足条件|g（x1）-g（x2）|≤4|x1-x2|的函数g（x）形成了一个集合M，其中x1，x2∈R，并且x12≤1，x22≤1，求函数y=f（x）=x2+3x-2（x∈R）与集合M的关系．
17．下列叙述能够组成集合的是（　　）
A．我校所有体质好的同学B．我校所有800米达标的女生
C．全国所有优秀的运动员D．全国所有环境优美的城市
1．设ω是1的虚立方根，且z1+ωz2+ω2z3=0，则以复数z1，z2，z3的对应点为顶点的三角形的形状是正三角形．
2．设a＞0，b＞0，a2+$\frac{{b}^{2}}{2}$=1，则4a•$\sqrt{1{+b}^{2}}$的最大值为（　　）
A．3$\sqrt{2}$B．3$\sqrt{5}$C．6D．没有最大值

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网