题目内容
(2013•东莞二模)已知函数g(x)=
ax3+2x2-2x,函数f(x)是函数g(x)的导函数.
(1)若a=1,求g(x)的单调减区间;
(2)若对任意x1,x2∈R且x1≠x2,都有f(
)<
,求实数a的取值范围;
(3)在第(2)问求出的实数a的范围内,若存在一个与a有关的负数M,使得对任意x∈[M,0]时|f(x)|≤4恒成立,求M的最小值及相应的a值.
| 1 |
| 3 |
(1)若a=1,求g(x)的单调减区间;
(2)若对任意x1,x2∈R且x1≠x2,都有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
(3)在第(2)问求出的实数a的范围内,若存在一个与a有关的负数M,使得对任意x∈[M,0]时|f(x)|≤4恒成立,求M的最小值及相应的a值.
分析:(1)求导数,利用导数小于0,可得函数的单调减区间.
(2)先f(
)<
用函数f(x)的表达式表示出来,再进行化简得-
(x1-x2)2<0,由此式即可求得实数a的取值范围;
(3)本小题可以从a的范围入手,考虑0<a<2与a≥2两种情况,结合二次的象与性质,综合运用分类讨论思想与数形结合思想求解.
(2)先f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| a |
| 4 |
(3)本小题可以从a的范围入手,考虑0<a<2与a≥2两种情况,结合二次的象与性质,综合运用分类讨论思想与数形结合思想求解.
解答:解:(1)当a=1时,g(x)=
x3+2x2-2x,g′(x)=x2+4x-2 …(1分)
由g′(x)<0解得-2-
<x<-2+
…(2分)
∴当a=1时函数g(x)的单调减区间为 (-2-
,2+
);…(3分)
(2)易知f(x)=g′(x)=ax2+4x-2
依题意知 f(
)-
=a(
)2+4×
-2-
=-
(x1-x2)2<0 …(5分)
因为x1≠x2,所以a>0,即实数a的取值范围是(0,+∞);…(6分)
(3)易知f(x)=ax2+4x-2=a(x+
)2-2-
,a>0.
显然f(0)=-2,由(2)知抛物线的对称轴x=-
<0 …(7分)
①当-2-
<-4即0<a<2时,M∈(-
,0)且f(M)=-4
令ax2+4x-2=-4解得 x=
…(8分)
此时M取较大的根,即M=
=
…(9分)
∵0<a<2,∴M=
=
>-1 …(10分)
②当-2-
≥-4即a≥2时,M<-
且f(M)=4
令ax2+4x-2=4解得 x=
…(11分)
此时M取较小的根,即 M=
=
…(12分)
∵a≥2,∴M=
=
≥-3当且仅当a=2时取等号 …(13分)
由于-3<-1,所以当a=2时,M取得最小值-3 …(14分)
| 1 |
| 3 |
由g′(x)<0解得-2-
| 6 |
| 6 |
∴当a=1时函数g(x)的单调减区间为 (-2-
| 6 |
| 6 |
(2)易知f(x)=g′(x)=ax2+4x-2
依题意知 f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
a
| ||||
| 2 |
=-
| a |
| 4 |
因为x1≠x2,所以a>0,即实数a的取值范围是(0,+∞);…(6分)
(3)易知f(x)=ax2+4x-2=a(x+
| 2 |
| a |
| 4 |
| a |
显然f(0)=-2,由(2)知抛物线的对称轴x=-
| 2 |
| a |
①当-2-
| 4 |
| a |
| 2 |
| a |
令ax2+4x-2=-4解得 x=
-2±
| ||
| a |
此时M取较大的根,即M=
-2+
| ||
| a |
| -2 | ||
|
∵0<a<2,∴M=
-2+
| ||
| a |
| -2 | ||
|
②当-2-
| 4 |
| a |
| 2 |
| a |
令ax2+4x-2=4解得 x=
-2±
| ||
| a |
此时M取较小的根,即 M=
-2±
| ||
| a |
| -6 | ||
|
∵a≥2,∴M=
-2±
| ||
| a |
| -6 | ||
|
由于-3<-1,所以当a=2时,M取得最小值-3 …(14分)
点评:本小题主要考查函数单调性的应用、导数在最大值、最小值问题中的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
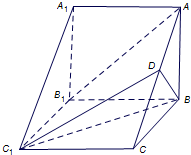 (2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.