题目内容
如图,圆 与圆
与圆 交于
交于 两点,以
两点,以 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆 和圆
和圆 于
于 两点,延长
两点,延长 交圆
交圆 于点
于点 ,延长
,延长 交圆
交圆 于点
于点 .已知
.已知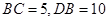 .
.
(1)求 的长;
的长;
(2)求 .
.
(1) ;(2)
;(2) .
.
解析试题分析:本题主要考查弦切角定理、三角形相似、切割线定理等基础知识,考查学生的逻辑推理能力、分析问题解决问题的能力.第一问,由于AC、AD分别是圆N、圆M的切线,所以利用弦切角定理,得到 ,
, ,所以相似三角形的判定,得△
,所以相似三角形的判定,得△ ∽△
∽△ ,所以可得到边的比例关系,从而求出边长;第二问,根据切割线定理,得到2组关系式,2个式子相除得到一个等式,再结合第一问的结论,解方程,得到
,所以可得到边的比例关系,从而求出边长;第二问,根据切割线定理,得到2组关系式,2个式子相除得到一个等式,再结合第一问的结论,解方程,得到 的值.
的值.
试题解析:(1)根据弦切角定理,知 ,
, ,
,
∴△ ∽△
∽△ ,则
,则 ,
,
故 . 5分
. 5分
(2)根据切割线定理,知 ,
, ,
,
两式相除,得 (*).
(*).
由△ ∽△
∽△ ,
,
得 ,
, ,又
,又 ,由(*)
,由(*)
得 . 10分
. 10分
考点:弦切角定理、三角形相似、切割线定理.

练习册系列答案
相关题目
 .
. :
: 与
与 轴相切,点
轴相切,点 的值;
的值; 轴上截得的弦长;
轴上截得的弦长; 是直线
是直线 上的动点,过点
上的动点,过点 与圆
与圆 为切点.求四边形
为切点.求四边形 面积的最小值。
面积的最小值。 中,以O为圆心的圆与直线
中,以O为圆心的圆与直线 相切.
相切. 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点 满足
满足 ,
, 的取值范围.
的取值范围. 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线 相切,求圆
相切,求圆 轴所得弦长为
轴所得弦长为 ;②被
;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为 ;③圆心到直线
;③圆心到直线 :
: 的距离为
的距离为 的圆的方程。
的圆的方程。 ,求该圆的方程.
,求该圆的方程.
 与圆
与圆 ,则
,则 上各点到
上各点到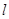 的距离的最小值为_____________。
的距离的最小值为_____________。