题目内容
已知圆 :
: 与
与 轴相切,点
轴相切,点 为圆心.
为圆心.
(1)求 的值;
的值;
(2)求圆 在
在 轴上截得的弦长;
轴上截得的弦长;
(3)若点 是直线
是直线 上的动点,过点
上的动点,过点 作直线
作直线 与圆
与圆 相切,
相切, 为切点.求四边形
为切点.求四边形 面积的最小值。
面积的最小值。
(1)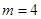 ;(2)
;(2)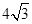 ;(3)
;(3)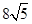
解析试题分析:(1)令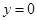 ,利用
,利用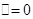 ,即可求出m的值
,即可求出m的值
(2)令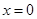 ,求出圆M在
,求出圆M在 轴上的两个交点的纵坐标之差的绝对值,即可求弦长;
轴上的两个交点的纵坐标之差的绝对值,即可求弦长;
(3)由题意知: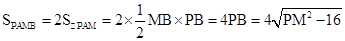 ,利用PM的最小值等于点M到直线
,利用PM的最小值等于点M到直线 的距离,即可求得结论
的距离,即可求得结论
(1)令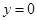 ,有
,有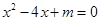 ,由题意知,
,由题意知,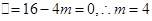
即 的值为4.
的值为4.
(2)设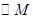 与
与 轴交于
轴交于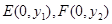 ,令
,令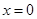 有
有 (
(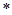 ),
),
则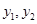 是(
是(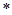 )式的两个根,则
)式的两个根,则 。
。
所以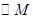 在
在 轴上截得的弦长为
轴上截得的弦长为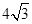
(3)由数形结合知:
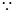 PM的最小值等于点M到直线
PM的最小值等于点M到直线 的距离即
的距离即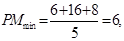
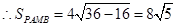 ,即四边形PAMB的面积的最小值为
,即四边形PAMB的面积的最小值为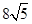 。
。
考点:直线与圆的位置关系

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
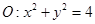 和圆
和圆 .
. 和圆
和圆 的位置关系;
的位置关系; ,求切线
,求切线 交圆
交圆 ,使得圆
,使得圆 ?若存在,求出圆
?若存在,求出圆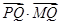 的最小值;
的最小值; +y2=1.过
+y2=1.过 轴上的动点
轴上的动点 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点. 的最大距离;
的最大距离;  时,求A,B两点坐标;
时,求A,B两点坐标; ,且被圆C:
,且被圆C: 截得的弦长等于8的直线方程。
截得的弦长等于8的直线方程。 与圆
与圆 交于
交于 两点,以
两点,以 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆 两点,延长
两点,延长 交圆
交圆 ,延长
,延长 交圆
交圆 .已知
.已知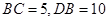 .
.
 的长;
的长; .
. 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆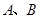 两点,且
两点,且 ,求圆
,求圆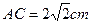 ,过C的割线CMN交
,过C的割线CMN交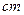 .
.