题目内容
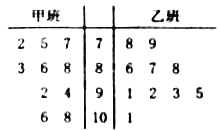
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
【答案】
(1)解:设Ai表示所取3人中有i个人评价该教师为“优秀”,
至多1人评价该教师为“优秀”记为事件A,
则P(A)=P(A0)+P(A1)= ![]() =
= ![]() .
.
(2)解:由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=( ![]() )3=
)3= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)=( ![]() )3=
)3= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =0.9.
=0.9.
【解析】(1)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多1人评价该教师为“优秀”记为事件A,由P(A)=P(A0)+P(A1),能求出至多有1人评价该教师是“优秀”的概率.(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及数学期望.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.