题目内容
已知椭圆 +
+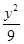 =1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
=1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
 +
+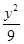 =1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
=1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )| A.1个 | B.2个 |
| C.3个 | D.0个 |
B
要使函数y=f(x)的图像能等分该椭圆的面积,则f(x)的图像应该关于椭圆的中心O对称,即f(x)为奇函数,①和②均满足条件.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 的左顶点
的左顶点 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与 轴的交点为
轴的交点为 ,已知
,已知 .
. 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点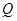 ,若
,若 轴上存在一定点
轴上存在一定点 ,使得
,使得 ,求椭圆的方程.
,求椭圆的方程.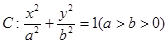 过点
过点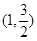 ,且离心率
,且离心率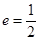 .
.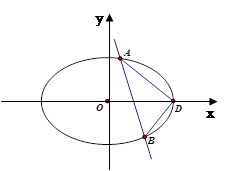
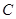 的标准方程;
的标准方程;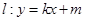 与椭圆
与椭圆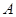 ,
,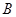 两点(
两点(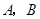 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为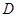 ,且满足
,且满足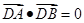 ,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.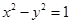 的焦点与椭圆
的焦点与椭圆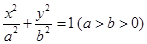 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为 ,
,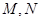 是椭圆上的的动点.
是椭圆上的的动点.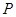 满足:
满足: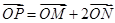 ,直线
,直线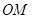 与
与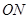 的斜率之积为
的斜率之积为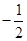 ,求证:存在定点
,求证:存在定点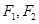 ,
,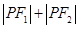 为定值,并求出
为定值,并求出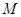 在第一象限,且点
在第一象限,且点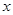 轴的射影为
轴的射影为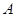 ,连接
,连接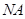 并延长交椭圆于
并延长交椭圆于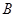 ,求证:以
,求证:以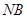 为直径的圆经过点
为直径的圆经过点 =1的左焦点为F1,右顶点为A,上顶点为B.若∠F1BA=90°,则椭圆的离心率是( )
=1的左焦点为F1,右顶点为A,上顶点为B.若∠F1BA=90°,则椭圆的离心率是( ) B.
B. C.
C. D.
D.


 ,+∞
,+∞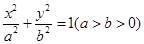 的离心率为
的离心率为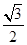 ,则双曲线
,则双曲线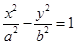 的渐近线方程是________
的渐近线方程是________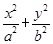 =1(a>b>0)的左、右焦点,B,C分别为椭圆的上、下顶点,直线BF2与椭圆的另一个交点为D,若cos∠F1BF2=
=1(a>b>0)的左、右焦点,B,C分别为椭圆的上、下顶点,直线BF2与椭圆的另一个交点为D,若cos∠F1BF2=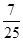 ,则直线CD的斜率为________.
,则直线CD的斜率为________.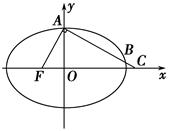
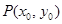 是椭圆
是椭圆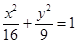 上一动点,
上一动点,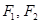 是椭圆的两个焦点,则
是椭圆的两个焦点,则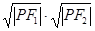 的最大值为
的最大值为