题目内容
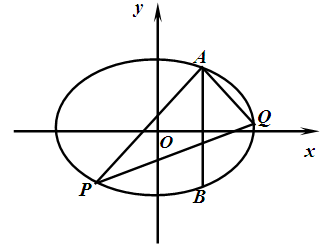
过椭圆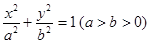 的左顶点
的左顶点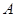 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与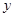 轴的交点为
轴的交点为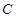 ,已知
,已知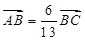 .
.
(1)求椭圆的离心率;
(2)设动直线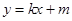 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点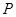 ,且与直线
,且与直线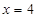 相交于点
相交于点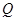 ,若
,若 轴上存在一定点
轴上存在一定点 ,使得
,使得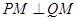 ,求椭圆的方程.
,求椭圆的方程.
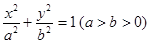 的左顶点
的左顶点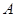 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与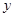 轴的交点为
轴的交点为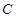 ,已知
,已知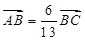 .
.(1)求椭圆的离心率;
(2)设动直线
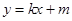 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点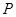 ,且与直线
,且与直线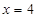 相交于点
相交于点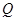 ,若
,若 轴上存在一定点
轴上存在一定点 ,使得
,使得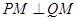 ,求椭圆的方程.
,求椭圆的方程.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(I)根据

 ,设直线方程为
,设直线方程为 ,
,
确定
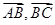 的坐标,由
的坐标,由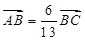 确定得到
确定得到 ,
,再根据
 点在椭圆上,求得
点在椭圆上,求得 进一步即得所求
进一步即得所求 ;
;(2)由
 可设
可设 ,
,得到椭圆的方程为
 ,
,由
 得
得
根据动直线
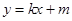 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P得到
 ,整理得
,整理得 .
.确定
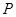 的坐标
的坐标 ,
,又
 ,
,

若
 轴上存在一定点
轴上存在一定点 ,使得
,使得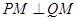 ,那么
,那么
可得
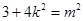 ,由
,由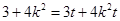 恒成立,故
恒成立,故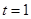 ,得解.
,得解.试题解析:(1)∵

 ,设直线方程为
,设直线方程为 ,
,
令
 ,则
,则 ,∴
,∴ , 2分
, 2分∴
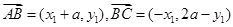 3分
3分∵
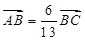 ,∴
,∴ =
= ,
,整理得
 4分
4分∵
 点在椭圆上,∴
点在椭圆上,∴ ,∴
,∴ 5分
5分∴
 即
即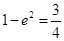 ,∴
,∴ 6分
6分(2)∵
 可设
可设 ,
,∴椭圆的方程为
 7分
7分由
 得
得 8分
8分∵动直线
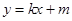 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P∴
 ,即
,即
整理得
 9分
9分设
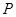
 则有
则有 ,
,
∴
 10分
10分又
 ,
,

若
 轴上存在一定点
轴上存在一定点 ,使得
,使得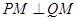 ,
,∴
 恒成立
恒成立 整理得
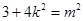 , 12分
, 12分∴
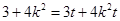 恒成立,故
恒成立,故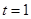
所求椭圆方程为
 13分
13分
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
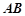 、
、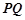 的四个端点都在椭圆
的四个端点都在椭圆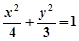 上,其中,直线
上,其中,直线 ,直线
,直线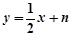 .
.
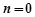 ,
,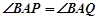 ,求
,求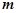 的值;
的值;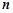 变化时,恒有
变化时,恒有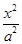 +
+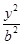 =1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4
=1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4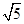 x的焦点重合,则椭圆的方程为( )
x的焦点重合,则椭圆的方程为( )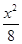 +
+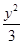 =1
=1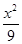 +
+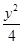 =1
=1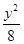 =1
=1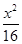 +
+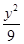 =1
=1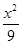 +
+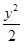 =1的焦点为F1、F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 .
=1的焦点为F1、F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 . 上有
上有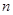 个不同的点
个不同的点 为右焦点,
为右焦点, 组成公差
组成公差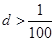 的等差数列,则
的等差数列,则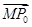 =
=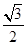
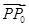 .
.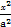 +
+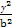 =1(a>b>0)的一个顶点A(2,0),离心率为
=1(a>b>0)的一个顶点A(2,0),离心率为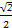 ,直线y=k(x-1)与椭圆C交于不同的两点M,N.
,直线y=k(x-1)与椭圆C交于不同的两点M,N.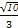 时,求k的值.
时,求k的值.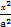 +
+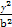 =1(a>b>0)的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM∥x轴,
=1(a>b>0)的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM∥x轴,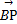 ·
·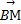 =9,若点P的坐标为(0,t),则t的取值范围是( )
=9,若点P的坐标为(0,t),则t的取值范围是( )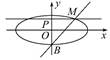

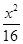 +
+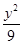 =1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
=1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )