题目内容
【题目】设函数f(x)=|x﹣1|+|x﹣2|
(1)求不等式f(x)≤3的解集;
(2)若不等式||a+b|﹣|a﹣b||≤|a|f(x)(a≠0,a∈R,b∈R)恒成立,求实数x的范围.
【答案】
(1)解: 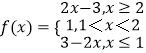 ,
,
所以解集[0,3]
(2)解:由||a+b|﹣|a﹣b||≤2|a|,
得2|a|≤|a|f(x),由a≠0,得2≤f(x),
解得x ![]() 或x
或x ![]()
【解析】(1)根据绝对值的代数意义,去掉函数f(x)=|x﹣1|+|x﹣2|中的绝对值符号,画出函数函数f(x)的图象,根据图象求解不等式f(x)≤3,(2)由||a+b|﹣|a﹣b||≤2|a|,得2|a|≤|a|f(x),由a≠0,得2≤f(x),从而解得实数x的范围.

练习册系列答案
相关题目